|
高中数学竞赛讲义(九) ──不等式 一、基础知识 不等式的基本性质: (1)a>b (3)a>b (5)a>b, c<0 (7)a>b>0, n∈N+ (9)a>0, |x|<a (10)a, b∈R,则|a|-|b|≤|a+b|≤|a|+|b|; (11)a, b∈R,则(a-b)2≥0 (12)x, y, z∈R+,则x+y≥2 前五条是显然的,以下从第六条开始给出证明。 (6)因为a>b>0, c>d>0,所以ac>bc, bc>bd,所以ac>bd;重复利用性质(6),可得性质(7);再证性质(8),用反证法,若 二、方法与例题 1.不等式证明的基本方法。 (1)比较法,在证明A>B或A<B时利用A-B与0比较大小,或把 例1 设a, b, c∈R+,试证:对任意实数x, y, z, 有x2+y2+z2 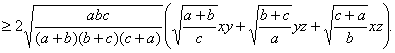 【证明】 左边-右边= x2+y2+z2 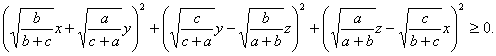 所以左边≥右边,不等式成立。 例2 若a<x<1,比较大小:|loga(1-x)|与|loga(1+x)|. 【解】 因为1-x 所以|loga(1+x)|>|loga(1-x)|. (2)分析法,即从欲证不等式出发,层层推出使之成立的充分条件,直到已知为止,叙述方式为:要证……,只需证……。 例3 已知a, b, c∈R+,求证:a+b+c-3 【证明】 要证a+b+c 因为 例4 已知实数a, b, c满足0<a≤b≤c≤ 【证明】 因为0<a≤b≤c≤ 所以 所以 所以只需证明 也就是证 只需证b(a-b) ≤a(a-b),即(a-b)2≥0,显然成立。所以命题成立。 (3)数学归纳法。 例5 对任意正整数n(≥3),求证:nn+1>(n+1)n. 【证明】 1)当n=3时,因为34=81>64=43,所以命题成立。 2)设n=k时有kk+1>(k+1)k,当n=k+1时,只需证(k+1)k+2>(k+2)k+1,即 所以由数学归纳法,命题成立。 (4)反证法。 例6 设实数a0, a1,…,an满足a0=an=0,且a0-2a1+a2≥0, a1-2a2+a3≥0,…, an-2-2an-1+an≥0,求证ak≤0(k=1, 2,…, n-1). 【证明】 假设ak(k=1, 2,…,n-1) 中至少有一个正数,不妨设ar是a1, a2,…, an-1中第一个出现的正数,则a1≤0, a2≤0,…, ar-1≤0, ar>0. 于是ar-ar-1>0,依题设ak+1-ak≥ak-ak-1(k=1, 2, …, n-1)。 所以从k=r起有an-ak-1≥an-1-an-2 ≥…≥ar-ar-1>0. 因为an≥ak-1≥…≥ar+1≥ar >0与an=0矛盾。故命题获证。 (5)分类讨论法。 例7 已知x, y, z∈R+,求证: 【证明】 不妨设x≥y, x≥z. ⅰ)x≥y≥z,则 ⅱ)x≥z≥y,则 (6)放缩法,即要证A>B,可证A>C1, C1≥C2,…,Cn-1≥Cn, Cn>B(n∈N+). 例8 求证: 【证明】 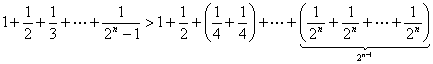 例9 已知a, b, c是△ABC的三条边长,m>0,求证: 【证明】 (7)引入参变量法。 例10 已知x, y∈R+, l, a, b为待定正数,求f(x, y)= 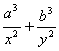 的最小值。 的最小值。【解】 设 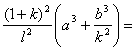 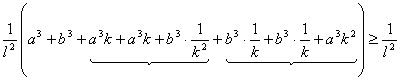 (a3+b3+3a2b+3ab2)= (a3+b3+3a2b+3ab2)=例11 设x1≥x2≥x3≥x4≥2, x2+x3+x4≥x1,求证:(x1+x2+x3+x4)2≤4x1x2x3x4. 【证明】 设x1=k(x2+x3+x4),依题设有 所以 ≤  ·3x2=4x2≤x2x3x4. ·3x2=4x2≤x2x3x4.所以原不等式成立。 (8)局部不等式。 例12 已知x, y, z∈R+,且x2+y2+z2=1,求证: 【证明】 先证 因为x(1-x2)= 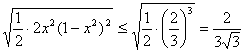 , ,所以 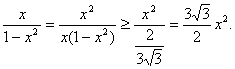 同理 所以 例13 已知0≤a, b, c≤1,求证: 【证明】 先证 即a+b+c≤2bc+2. 即证(b-1)(c-1)+1+bc≥a. 因为0≤a, b, c≤1,所以①式成立。 同理 三个不等式相加即得原不等式成立。 (9)利用函数的思想。 例14 已知非负实数a, b, c满足ab+bc+ca=1,求f(a, b, c)= 【解】 当a, b, c中有一个为0,另两个为1时,f(a, b, c)= 因为1=(a+b)c+ab≤ 解关于a+b的不等式得a+b≥2( 考虑函数g(t)= 又因为0≤c≤ 所以f(a, b, c)= ≥  = = 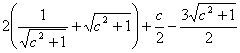 ≥ 下证 所以f(a, b, c) ≥ 2.几个常用的不等式。 (1)柯西不等式:若ai∈R, bi∈R, i=1, 2, …, n,则 等号当且仅当存在λ∈R,使得对任意i=1, 2, , n, ai=λbi, 变式1:若ai∈R, bi∈R, i=1, 2, …, n,则 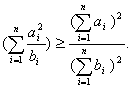 等号成立条件为ai=λbi,(i=1, 2, …, n)。 变式2:设ai, bi同号且不为0(i=1, 2, …, n),则 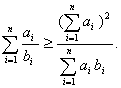 等号成立当且仅当b1=b2=…=bn. (2)平均值不等式:设a1, a2,…,an∈R+,记Hn= 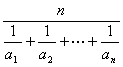 , Gn= , Gn=其中等号成立的条件均为a1=a2=…=an. 【证明】 由柯西不等式得An≤Qn,再由Gn≤An可得Hn≤Gn,以下仅证Gn≤An. 1)当n=2时,显然成立; 2)设n=k时有Gk≤Ak,当n=k+1时,记 因为a1+a2+…+ak+ak+1+(k-1)Gk+1≥ ≥ 所以a1+a2+…+ak+1≥(k+1)Gk+1,即Ak+1≥Gk+1. 所以由数学归纳法,结论成立。 (3)排序不等式:若两组实数a1≤a2≤…≤an且b1≤b2≤…≤bn,则对于b1, b2, …, bn的任意排列 【证明】 引理:记A0=0,Ak= 证法一:因为b1≤b2≤…≤bn,所以 记sk= 所以 最后一个不等式的理由是aj-aj+1≤0(j=1, 2, …, n-1, sn=0), 所以右侧不等式成立,同理可证左侧不等式。 证法二:(调整法)考察 若 因为 所 调整后,和是不减的,接下来若 例15 已知a1, a2,…,an∈R+,求证; 【证明】证法一:因为 上述不等式相加即得 证法二:由柯西不等式 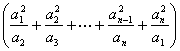 (a1+a2+…+an)≥(a1+a2+…+an)2, (a1+a2+…+an)≥(a1+a2+…+an)2,因为a1+a2+…+an >0,所以 证法三: 设a1, a2,…,an从小到大排列为 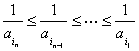 ,由排序原理可得 ,由排序原理可得注:本讲的每种方法、定理都有极广泛的应用,希望读者在解题中再加以总结。 三、基础训练题 1.已知0<x<1,a, b∈R+,则 2.已知x∈R+,则 3.已知a, b, c∈R,且a2+b2+c2=1, ab+bc+ca的最大值为M,最小值为N,则MN=___________. 4.若不等式 5.若不等式 6.“a+b=4”是“不等式|x-a|+|x-b|<8的解集是{x|-2<x<6}”的____________条件. 7.若a, b∈R+,则a+b=1,以下结论成立是__________.① a4+b4≥ 8.已知0< 9.已知 10.已知a>0, b>0且a 11.已知n∈N+,求证: 12.已知0<a<1,x2+y=0,求证:loga(ax+ay) ≤loga2+ 13.已知x∈R, 四、高考水平训练题 1.已知A=asin2x+bcos2x, B=acos2x+bsin2x(a, b, x∈R),设m=AB, n=ab, P=A2+B2, q=a2+b2,则下列结论成立的有]__________.(1)m≥n, p≥q;(2)m≤n, p≤q;(3)m+p≥n+q;(4)m+q≥n+p. 2.已知a, b, c, d∈R,M=4(a-b)(c-d), N=(a-b)(c-b)+(d-a)(d-c)+(c-d)(c-b)+(a-b)(a-d),则比较大小:M________N. 3.若 4.已知△ABC的三边长a, b, c满足b+c≤2a, a+c≤2b,则 5.若实数x, y满足|x|+|y|≤1,则z=x2-xy+y2的最大值与最小值的和为________. 6.设函数f(x)= 7.对x1>x2>0, 1>a>0,记 8.已知函数 9.设a≤b<c是直角△ABC 的三边长,若不等式 10.实系数方程x2+ax+2b=0的一个根大于0且小于1,另一个根大于1且小于2,则 11.已知a, b, c∈R+且满足 a+b+c≥abc,求证:下列三个式子中至少有两个成立: 12.已知a, b∈R+且 13.已知a, b, c ∈R+,求证: 14.设x, y, z是3个不全为零的实数,求 五、联赛一试水平训练题 1.已知a1, a2, b1, b2, c1, c∈R,a1c1- 2.已知x2+y2-xy=1,则|x+y-3|+|x+y+2|=__________. 3.二次函数f(x)=x2+ax+b,记M=max{|f(1)|, |f(2)|, |f(3)|},则M的最小值为__________. 4.设实数a, b, c, d满足a≤b≤c≤d或者a≥b≥c≥d,比较大小: 4(a+c+d)(a+b+d)__________(2a+3d+c)(2a+2b+c+d). 5.已知xi∈R+, i=1, 2, …,n且 6.已知x, y∈R, f(x, y)=x2+6y2-2xy-14x-6y+72的最小值为__________. 7.已知0≤ak≤1(k=1, 2, …,2n),记a2n+1=a1, a2n+2=a2,则 8.已知0≤x≤1, 0≤y≤1, 0≤z≤1,则 9.已知 10.对于不全相等的正整数a, b, c,求证: 11.已知ai>0(i=1, 2, …, n),且 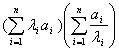 ≤ ≤六、联赛二试水平训练题 1.设正实数x, y, z满足x+y+z=1,求证:  2.设整数x1, x2, …,xn与y1, y2, …, yn满足1<x1<x2<…<xn<y1<y2<…<ym, x1+x2+…+xn>y1+y2+…+ym,求证:x1x2xn>y1y2…ym. 3.设f(x)=x2+a,记 4.给定正数λ和正整数n(n≥2),求最小的正数M(λ),使得对于所有非负数x1, x2,…,xn ,有M(λ) 5.已知x, y, z∈R+,求证:(xy+yz+zx) 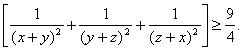 6.已知非负实数a, b, c满足a+b+c=1,求证:2≤(1-a2)2+(1-b2)2+(1-c2)2≤(1+a)(1+b)(1+c),并求出等号成立的条件。 本系列讲座由在人教中数论坛网友“0.1”整理提供,感谢他(她)的分享。 (责任编辑:admin) |
