|
2007年台湾数学能力竞赛决赛 1. 试求使 2. 3. 锐角 4. 给定 5. 有一正整数列1,2,3,…,2n-1、2n,现从中挑出n个数,从大到小排列依次为a1,a2,…,an,另n个数从小到大排列依次为b1,b2,…,bn,求 6. a、b、c为正实数,试证明: 参考答案: 1. 引理: 设 因 则 故 故共有8组解 2. 设 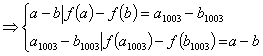 故 又 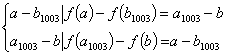 故 欲使(1)(2)同时成立,唯有 3. 作三高之垂足,显然成立。  设三垂足分别为D 0,E 0,F 0,若有一D异于D 0合条件,欲使 于是,若D在D 0左侧,则E,F也在左侧 若在右侧亦然,故D 0,E 0,F 0为唯一。 4. 设 由正弦定理,   5. 令n+1、n+2、n+3、…、2n为大数,1、2、3、…、n为小数。 设 其中 令a1,a2,…,ak,bk+1,b k+2,…,bn为大数, b1,b2,…,bk,ak+1,a k+2,…,an为小数。  6. 令 当  时,不等式恒成立, 时,不等式恒成立,故  , ,同理 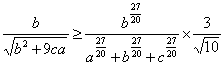 , , 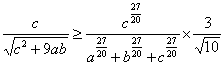 则 (责任编辑:admin) |
