|
《3.3 几何概型》测试题 一、选择题 1.(2011·福建文)如图，矩形ABCD中，点E为边CD的中点，若在矩形ABCD内部随机取一个点Q，则点Q取自△ABE内部的概率等于( ). 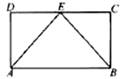 A.  B. C. D. 考查目的：考查几何概型的意义及其概率计算. 答案：C. 解析：所求概率为  ，故答案选C.2.(2012·辽宁理)在长为12cm的线段AB上任取一点C．现作一矩形，其边长分别等于线段AC，CB的长，则该矩形面积小于32  的概率为( ).A.  B. C. D. 考查目的：考查函数模型的应用、不等式的解法、几何概型的计算，以及分析问题的能力. 答案：C. 解析：设线段AC的长为  cm，则线段CB的长为 cm，矩形的面积为 ，由 解得 或 .又∵ ，∴该矩形面积小于32的概率为，故选C.3.(2012·北京理)设不等式组  表示的平面区域为D.在区域D内随机取一个点，则此点到坐标原点的距离大于2的概率是 ( ).A.  B. C. D. 考查目的：不等式组表示平面区域以及几何概型的计算. 答案：D.  解析：题目中 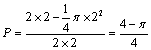表示的区域表示正方形区域，而动点D可以存在的位置为正方形面积减去四分之一的圆的面积部分，因此 ，故选D.二、填空题 4.(2010·湖南文)在区间[-1，2]上随机取一个数 ，则 的概率为 .考查目的：考查与长度有关的几何概型问题的概率计算. 答案： .解析：区间[0，1]的两端点之间长度是1，区间[-1，2]的长度是3，故  的概率是.5.已知下图所示的矩形，其长为12，宽为5.在矩形内随机地撒1 000颗黄豆，数得落在阴影部分的黄豆数为550颗，则可以估计出阴影部分的面积约为 .  考查目的：了解随机数的概念，与面积有关的几何概型概率问题. 答案：33. 解析：设阴影部分的面积为S，由条件知矩形面积为60，则  ，解得 .6.将一条5米长的绳子随机地切断成两条，事件T表示所切两段绳子都不短于1米的事件，事件T发生的概率 . 考查目的：考查随机事件是否为几何概型的判断. 答案：  .解析：类似于古典概型，先找到基本事件组，既找到其中每一个基本事件.注意到每一个基本事件都与唯一一个断点一一对应，故基本事件组中的基本事件就与线段上的点一一对应，若把离绳首尾两端距离为1的点记作M、N，则显然事件T所对应的基本事件所对应的点在线段MN上.由于在古典概型中事件T的概率为T包含的基本事件个数/总的基本事件个数，但这两个数字(T包含的基本事件个数、总的基本事件个数)是无法找到的，所以用线段MN的长除以线段AB的长表示事件T的概率，即  .三、解答题 7.如图，在单位圆O的某一直径上随机的取一点Q，求过点Q且与该直径垂直的弦长长度不超过1的概率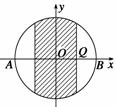．  考查目的：考查几何概型问题的概率计算，以及对立事件概率计算等. 答案：  .解析：弦长不超过1，即 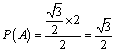 ，而Q点在直径AB上是随机的，事件 .由几何概型的概率公式得 .∴弦长不超过1的概率为  .8.甲、乙两人约定在6时到7时之间在某处会面，并约定先到者应等候另一人一刻钟，过时即可离去，求两人能会面的概率. 考查目的：考查将实际问题转化为几何概型概率问题解决的能力. 答案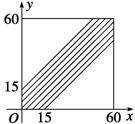：  . 解析：以 轴和 轴分别表示甲、乙两人到达约定地点的时间，则两人能够会面满足的条件是 .在如图所示平面直角坐标系下，(，)的所有可能结果是边长为60的正方形区域，而事件A“两人能够会面”的可能结果由图中的阴影部分表示.由几何概型的概率公式得 .(责任编辑：admin) |