|
3.3 几何概型 重难点：掌握几何概型中概率的计算公式并能将实际问题转化为几何概型，并正确应用几何概型的概率计算公式解决问题． 考纲要求：①了解几何概型的意义，并能正确应用几何概型的概率计算公式解决问题． ②了解随机数的意义，能运用模拟方法估计概率． 经典例题：如图，  ， ， ，在线段 上任取一点 ， 试求：(1) 为钝角三角形的概率；(2)为锐角三角形的概率．当堂练习： 1．从一批羽毛球产品中任取一个，其质量小于4.8g的概率为0.3，质量小于4.85g的概率为0.32，那么质量在[4.8，4.85]（g）范围内的概率是（ ） A．0.62 B．0.38 C．0.02 D．0.68 2．在长为10 cm的线段AB上任取一点P，并以线段AP为边作正方形，这个正方形的面积介于25 cm2与49 cm2之间的概率为（ ） A．  B． C． D． 3．同时转动如图所示的两个转盘，记转盘甲得到的数为x，转盘乙得到的数为y，构成数对（x，y），则所有数对（x，y）中满足xy＝4的概率为（ ） A．  B． C． D．  4．如图，是由一个圆、一个三角形和一个长方形构成的组合体，现用红、蓝两种颜色为其涂色，每个图形只能涂一种颜色，则三个形状颜色不全相同的概率为（ ）  A．  B． C． D． 5．两人相约7点到8点在某地会面，先到者等候另一人20分钟，过时离去．则 求两人会面的概率为（ ） A．  B． C． D． 6如图，某人向圆内投镖，如果他每次都投入圆内，那么他投中正方形区域的概率为（ ）  A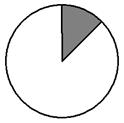． B． C．  D． 7．如图，有一圆盘其中的阴影部分的圆心角为 ，若向圆内投镖，如果某人每次都投入圆内，那么他投中阴影部分的概率为（ ）A． B． C．  D．8．现有  的蒸馏水，假定里面有一个细菌，现从中抽取 的蒸馏水，则抽到细菌的概率为 （ ）A．  B． C． D．9．一艘轮船只有在涨潮的时候才能驶入港口，已知该港口每天涨潮的时间为早晨  至 和下午至 ，则该船在一昼夜内可以进港的概率是（ ）A．  B． C． D． 10．在区间  中任意取一个数，则它与 之和大于 的概率是（ ） A．  B． C．  D． 11．若过正三角形  的顶点 任作一条直线 ，则与线段 相交的概率为（ ）A．  B． C．  D．12．在500ml的水中有一个草履虫，现从中随机取出2ml水样放到显微镜下观察，则发现草履虫的概率是（ ） A．0.5 B．0.4 C．0.004 D．不能确定 13．平面上画了一些彼此相距2a的平行线，把一枚半径r<a的硬币任意掷在这个平面上，求硬币不与任何一条平行线相碰的概率（ c ） A．  B． C．  D． 14．已知地铁列车每10min一班，在车站停1min．则乘客到达站台立即乘上车的概率为 ． 15．随机向边长为2的正方形ABCD中投一点P,则点P与A的距离不小于1且与  为锐角的概率是__________________．16．在区间(0,1)中随机地取出两个数，则两数之和小于  的概率是 ．17．假设你家订了一份报纸，送报人可能在早上6：30～7：30之间把报纸送到你家，你父亲离开家去上班的时间为早上7：00～8：00之间，你父亲在离开家前能拿到报纸的概率为_______． 18．飞镖随机地掷在下面的靶子上． （1）在靶子1中，飞镖投到区域A、B、C的概率是多少？ （2）在靶子1中，飞镖投在区域A或B中的概率是多少？在靶子2中，飞镖没有投在区域C中的概率是多少？  19．一只海豚在水池中游弋，水池为长  ，宽 的长方形，求此刻海豚嘴尖离岸边不超过 的概率．20．在长度为10的线段内任取两点将线段分为三段，求这三段可以构成三角形的概率． 21．利用随机模拟方法计算曲线  ， ， 和 所围成的图形的面积．参考答案： 经典例题：解：如图，由平面几何知识： 当  时， ；当  时， ， ．（１）当且仅当点  在线段 或 上时， 为钝角三角形记＂ 为钝角三角形＂为事件 ，则 即 为钝角三角形的概率为 ．（２）当且仅当点 在线段 上时，为锐角三角，记＂ 为锐角三角＂为事件 ，则 即 为锐角三角形的概率为 ．当堂练习： 1.B; 2.B; 3.C; 4.A; 5.C; 6.A; 7.A; 8.B; 9.C; 10.C; 11.C; 12.B; 13.B; 14. 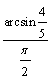 ; 15.  ; 16.  ; 17. 87.5%;18.（1）都是  ；（2） 。19.解：由已知可得，海豚的活动范围在26×16㎡的区域外， 所以海豚嘴尖离岸边不超过  的概率为 。20.解：设构成三角形的事件为A，长度为10的线段被分成三段的长度分别为x，y， 10－（x＋y）， 则  ，即 ．由一个三角形两边之和大于第三边，有  ，即 ． 又由三角形两边之差小于第三边，有  ，即 ，同理 ． ∴ 构造三角形的条件为  ．∴ 满足条件的点P（x，y）组成的图形是如图所示中的阴影区域（不包括区域的边界）．  ， ．∴  ．
21. 解：（１）利用计算器或计算机产生两组  到 区间上的随机数， ， ；（２）进行平移变换：  ；（其中 分别为随机点的横坐标和纵坐标）（３）数出落在阴影内的点数  ，用几何概型公式计算阴影部分的面积．例如，做  次试验，即 ，模拟得到 ，所以  ，即 ．(责任编辑：admin) |
