|
《1.3 空间几何体的表面积和体积》测试题 一、选择题 1.(2010福建文)若一个底面是正三角形的三棱柱的正视图如图所示，则其侧面积等于( ).  A.  B.2 C. D.6考查目的：考查立体几何中的三视图，识图的能力、空间想象能力等基本能力. 答案：D. 解析：由正视图知：三棱柱是以底面边长为2，高为1的正三棱柱，∴底面积为  ，侧面积为 ．2.(2011辽宁文)一个正三棱柱的侧棱长和底面边长相等，体积为 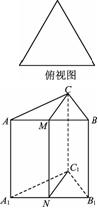，它的三视图中的俯视图如图所示，左视图是一个矩形，则这个矩形的面积是( ). A.4 B. C.2 D.考查目的：考查立体几何中的三视图与几何体的转换以及相应线段的转化关系. 答案：B. 解析：由俯视图知该正三棱柱的直观图为下图，其中M，N是中点，矩形  为左视图.设棱长为  ，∵体积为，∴ ，解得 ，∴ ，∴矩形面积为.3.(2011湖南文)如图是某几何体的三视图，则该几何体的体积为( ). 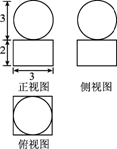 A.  B. C. D. 考查目的：考查组合体体积的求解. 答案：D. 解析：由三视图知这个几何体由上面是一个直径为3的球，下面是一个长、宽都为3，高为2的长方体所构成的几何体，其体积   .二、填空题 4.(2012上海文)一个高为2的圆柱，底面周长为  ，该圆柱的表面积为 .考查目的：考查圆柱的表面积. 答案：  .解析：∵底面圆的周长  ，∴圆柱的底面半径 ，∴圆柱的侧面积为 ，两个底面积为 ，∴圆柱的表面积为.5.(2009浙江)若某几何体的三视图(单位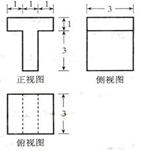：  )如图所示，则此几何体的体积是  . 考查目的：考查根据三视图求几何体体积. 答案：18. 解析：该几何体是由二个长方体组成，下面体积为  ，上面的长方体体积为 ，因此其几何体的体积为18.6.(2011安徽)一个空间几何体的三视图如图所示，则该几何体的表面积为 . 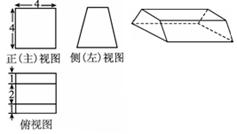 考查目的：考查根据三视图求几何体表面积.. 答案：  .解析：由三视图可知本题所给的是一个底面为等腰梯形的放倒的直四棱柱(如图所示)，∴该直四棱柱的表面积为  .三、解答题： 7.(2011湖北改编) 设球的表面积为  ，体积为 ，它的内接正方体的表面积为 ，体积为 ，求 ， .考查目的：考查球和正方体的表面积和体积计算，比较球和其内接正方体的表面积、体积之间的关系. 答案：  ， .解析：设球的半径为  ，则 ， .设正方体的边长为，则 ， .又∵ ，∴ ， ，即 ， .8.已知：一个圆锥的底面半径为 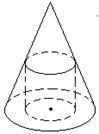，高为 ，在其中有一个高为 的内接圆柱. ⑴求圆柱的侧面积； ⑵ 为何值时，圆柱的侧面积最大.考查目的：考查几何体的侧面积的计算，考查对组合体的分析能力，空间想象能力及推理运算能力. 答案：⑴  ；⑵ .解析：⑴设内接圆柱底面半径为  ， ，∵ ，∴ .②代入①得 ；⑵   ，∴当 时， .(责任编辑：admin) |