|
第三章《函数的应用》复习测试题（一） 一、选择题 1.(2012北京)函数  的零点个数为( ).A.0 B.1  C.2 D.3考查目的：考查函数零点的概念、函数的单调性和数形结合思想. 答案：B. 解析：(方法1)：令  得，  ，在平面直角坐标系中分别画出幂函数 和指数函数 的图象，可知它们只有一个交点，∴函数的零点只有一个.(方法2)：∵函数 在 上单调递增，且 ，∴函数的零点只有一个.答案选B.2.(2010天津)函数  的零点所在的一个区间是( ).A.(-2，-1) B.(-1，0) C.(0，1) D.(1，2)考查目的：考查函数零点的存在性定理. 答案：B 解析：∵  ， ，∴答案选B.3.(2009福建)若函数  的零点与 的零点之差的绝对值不超过0.25， 则可以是( ).A.  B. C. D. 考查目的：考查函数零点的概念和零点存在性定理. 答案：A. 解析： 的零点为 ，的零点为 ，的零点为 ， 的零点为 .下面估算的零点. ∵ ， ，∴ 的零点 .依题意，函数的零点与的零点之差的绝对值不超过0.25，∴只有的零点符合题意，故答案选A.4.在研制某种新型材料过程中，实验人员获得了下列一组实验数据，现准备用下列四个函数中的一个近似地表示这些数据的规律，其中最接近的一个是( ).
A.  B. C. D. 考查目的：考查几类不同增长类型函数模型与实际问题的拟合程度. 答案：D. 解析：通过检验可知，只有函数 较为接近，故答案选D.5.已知函数  ， ， 的零点分别为 ， ，则 的大小关系是( ).A.  B. C.  D. 考查目的：考查函数零点的定义，指数函数、对数函数、幂函数、一次函数的图象，以及数形结合思想. 答案：C. 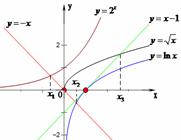 解析：由已知得，  ，在同一平面直角坐标系中，画出函数 的图象，由图象可知，，故答案选C.6.(2010陕西)某学校要召开学生代表大会，规定各班每10人推选一名代表，当各班人数除以10的余  数大于6时再增选一名代表.那么，各班可推选代表人数 与该班人数 之间的函数关系用取整函数 ( 表示不大于的最大整数)可以表示为( ).A.  B. C. D. 考查目的：考查函数的建模及其实际应用，意在考查分析问题与解决问题的能力. 答案：B. 解析：(方法1)：当 除以 的余数0，1，2，3，4，5，6时，由题设知，且易验证，此时 .当除以10的余数为7，8，9时，由题设知 ，易验证，此时 .综上得，必有 ，故选B.(方法2)：依题意知：若  ，则 ，由此检验知选项C，D错误.若 ，则 ，由此检验知选项A错误.故由排除法知，本题答案应选B.二、填空题 7.(2009浙江)某地区居民生活用电分为高峰和低谷两个时间段进行分时计价．该地区的电网销售电价表如下：
若某家庭5月份的高峰时间段用电量为  千瓦时，低谷时间段用电量为 千瓦时，则按这种计费方式，该家庭本月应付的电费为 元(用数字作答).考查目的：考查分段函数在解决实际问题中的应用. 答案：  .解析：该家庭本月应付电费由两部分构成：高峰部分为  ，低谷部分为  ，这两部分电费之和为(元).8.(2009山东)若函数  有两个零点，则实数 的取值范围是__________．考查目的：考查函数零点的定义，指数函数与一次函数的图象，数形结合的思想. 答案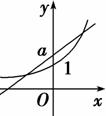：  . 解析：设函数  和函数 ，则函数有两个零点，就是函数的图象与函数的图象有两个交点.由图象可知，当 时，两个函数的图象只有一个交点，不符合题意；当 时，∵函数的图象过点(0，1)，而直线所过的点一定在点(0，1)的上方，∴两个函数的图象一定有两个交点，∴实数的取值范围是 .9.某电脑公司2012年的各项经营收入中，经营电脑配件的收入为400万元，占全年经营总收入的40%.该公司预计2014年经营总收入要达到1690万元，且计划从2012年到2014年，每年经营总收入的年增长率相同，则2013年预计经营总收入为________万元. 考查目的：考查增长率模型在实际问题中的应用和读题审题能力. 答案：1300. 解析：设年平均增长率为 ，则 ，∴ ，∴2013年预计经营总收入为 × ＝1300(万元).10.(2010全国I理15改编)若函数  有四个零点，则实数的取值范围是 .考查目的：考查函数零点的定义，函数的图象与性质、不等式的解法，和数形结合思想. 答案：  .解析：在平面直角坐标系内，先画函数  的图象.当 时， ，图象的顶点为 ，与轴交于点(0，-1)；当 时， ，图象的顶点为 ，与轴交于点(0，-1). 是一条与轴平行的直线.当 时，直线与函数的图象有4个交点，即当 ，函数有四个零点.11.为了预防流感，某段时间学校对教室用药熏消毒法进行消毒.设药物开始释放后第 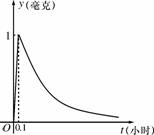 小时教室内每立方米空气中的含药量为毫克.已知药物释放过程中，教室内每立方米空气中的含药量(毫克)与时间(小时)成正比.药物释放完毕后，与的函数关系式为 (为常数).函数图象如图所示.则从药物释放开始，每立方米空气中的含药量(毫克)与时间(小时)之间的函数关系式为 . 考查目的：考查待定系数法求指数函数、一次函数解析式的方法，以及阅读理解能力和分类讨论思想. 答案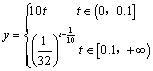：  .解析：函数图象由一条线段与一段指数函数图象组成，它们的交点为(0.1，1).当 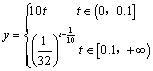 时，由(毫克)与时间 (小时)成正比设 ，∴ ，解得 ，∴ .当 时，将(0.1，1)代入 得 ，∴ ， ，∴函数关系式为.(责任编辑：admin) |
||||||||||||||||||||||||||||||||