|
南昌市高中新课程复习训练题数学（集合与简易逻辑） 命题：南昌十九中 陈平 一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的。 1、设P，Q为两个非空实数集合，定义集合P+Q={a+b|, a∈P，b∈Q}，若P={0，2，5}，Q={1，2，6}，则P+Q中元素的个数是（ ） A.9 B.8 C.7 D.6 2、若集合M=｛y| y=  ｝，P=｛y| y= ｝，则M∩P= （ ）A｛y| y>1｝ B｛y| y≥1｝ C｛y| y>0｝ D｛y| y≥0｝ 3、下列四个集合中，是空集的是 ( ) A .  B . C. { D . .4、若关于x的不等式  <1的解集为{x|x <1或x > 2},则实数a的值为( )A.1 B.0 C.2 D.  5、已知集合M=｛a2, a+1,-3｝, N=｛a-3, 2a-1, a2+1｝, 若M∩N=｛-3｝, 则a的值是 ( ) A -1 B 0 C 1 D 2 6、设集合A={x|  < 0},B={x||x-1|<a},则“a=1”是“A∩B≠ ”的（ ）A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分又不必要条件 7、50名学生参加跳远和铅球两项测试，跳远、铅球测试及格的分别有40人和31人，两项测试均不及格的有4人，两项测试全都及格的人数是（ ） A.35 B.25 C.28 D.15 8、一元二次方程  有一个正根和一个负根的充分不必要条件是：（ ）A．  B． C． D． 9、若二次不等式ax2+bx+c > 0的解集是{x|  < x < },那么不等式2cx2-2bx-a < 0的解集是( )A.{x|x< -10或x > 1} B.{x|－ < x <} C.{x|4< x <5} D.{x|-5< x < -4}10、已知函数f(x)在(-∞,+∞)上为增函数,a,b∈R,对于命题“若a+b≥0，则f(a)+f(b)≥f(-a)+f(-b)”有下列结论: ①此命题的逆命题为真命题 ②此命题的否命题为真命题 ③此命题的逆否命题为真命题 ④此命题的逆命题和否命题有且只有一个真命题 其中正确结论的个数为( ) A.1个 B.2个 C.3个 D.4个 11、对任意实数  , 若不等式 恒成立, 则实数 的取值范围是 ( )A k≥1 B k <1 C k≤1 D k >1 12、若集合A  B, AC, B=｛0,1,2,3,4,7,8｝, C=｛0,3,4,7,8｝, 则满足条件的集合A的个数为( )A. 16 B 15 C 32 D 31 二、填空题：本大题共4小题；每小题4分，共16分，把答案填在题中的横线上。 13、已知全集U  ，A ，B ，那么 ___14、若集合A={x∈R|ax2+x+2=0，a∈R}至多含有一个元素，则a的取值范围是 。 15、有甲、乙、丙、丁四位歌手参加比赛，其中有一位获奖，有人走访了四位歌手，甲说：“我获奖了”，乙说：“甲、丙未获奖”，丙说：“是甲或乙获奖”，丁说：“是乙获奖”。四位歌手的话有两句是对的，则是 歌手获奖 16、设二次函数  ，若 （其中 ），则 等于 _____.三、解答题：本大题共6小题，共74分，解答应写出文字说明，证明过程或推演步骤。 17、设全集U=R, 集合A=｛x| x2- x-6<0｝, B=｛x|| x|= y+2, y∈A｝, 求CUB、A∩B、A∪B、CU(A∪B), (CUA)∩(CUB).。 18、若不等式  的解集为 ，求 的值19、已知P：2x2-9x+a < 0,q：  且 p是q的充分条件,求实数a的取值范围.20、用反证法证明：已知  ，且 ，则 中至少有一个大于1。.21、已知集合A  ，B ，且 ，求实数 的值组成的集合。22、（本小题14分）已知a > 0,a≠1,设p:函数y =loga(x+1)在(0,∞)上单调递减;q:曲线y = x2+(2a-3)x+1与x轴交于不同的两点,如果p且q为假命题,p或q为真命题,求a的取值范围. 南昌市高中新课程方案试验高三复习训练题 数学（一）参考答案 一、选择题 1、B 2、C 3、D 4、D 5、A 6、A 7、B 8、D 9、A 10、C 11、B 12、C 二、填空题 13．  , 14．｛0｝或｛a︱a≥ ｝ 15．甲 16． 三、解答题 17．解:A=(-2,3), ∵-2<x <3, ∴0<|x|<5. ∴B=(-5,0)∪(0,5). ∴CUB=  ,A∩B=(-2,0)∪(0,3), A∪B=(-5,5), , CU(A∪B)=( CUA)∩(CUB)=  ∪ 18．由题意知方程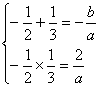  的两根为 ，又  ，即 ，解得 ，   19.解由 x2-4x+3<0 得 1<x<3 即2<x<3x2-6x+8<0 2<x<4 ∴q:2<x<3 设A=｛ ︱p｝=｛︱2x2-9x+a<0｝B=｛ ︱q｝=｛︱2<x<3｝p q, ∴ qp ∴BA即2<x<3满足不等式 2x2-9x+a<0 ∴2<x<3满足不等式 a<9x-2x2 ∵当2<x<3时，9x-2x2=-2(x2-  x+ -)=-2(x-  )2+ 的值大于9且小于等于，即9<9x-2x2≤ ∴a≤9 20. 假设 均不大于1，即 ，这与已知条件 矛盾 中至少有一个大于121.  ①  ；②  时，由 。 所以适合题意的 的集合为 ① ；② 时，由。所以适合题意的 的集合为① ；② 时，由。所以适合题意的 的集合为22.解：由题意知p与q中有且只有一个为真命题， 当0<a<1时，函数  在（0，+∞）上单调递减；当a>1，函数 在（0，+∞）上不是单调递减；曲线y=x2+(2a-3)x+1与x轴交于两点等价于（2a-3）2-4>0，即a< 或a> （1）若p正确，q不正确，即函数 在（0，+∞）上单调递减，曲线y=x2+(2a-3)x+1与x轴不交于两点， 因此a∈（0，1）∩（[ ，1]∪（1，）），即a∈ （2）若p不正确,q正确,即函数y=loga(x+1)在（0,+∞）上不是单调递减, 曲线y=x2+(2a-3)x+1与x轴交于两点, 因此a∈（1,+∞）∩（（0, ）∪（,+∞）） 即a∈（，+∞）综上，a取值范围为[ ，1)∪(，+∞)(责任编辑：admin) |