|
教科书第57页上的第一段是否证明了一个命题“两条曲线有交点的充要条件是它们的方程所组成的方程组有实数解?” 是的。这一段话是叙述式的,我们也可以将它规范化:设曲线C1,C2的方程分别为f1(x,y)=0,f2(x,y)=0 。 (1)充分性。要证明:如果方程组 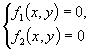 有实数解,那么C1,C2有交点。 设x=x0,y=y0为方程组(1)的实数解,则f1(x0,y0)=0,f2(x0,y0)=0 。即点P(x0,y0)既在C1上,又在C2上,所以它是C1,C2的交点。 (2)必要性。要证明:如果C1,C2有交点,那么方程组(1)有实数解。 设C1,C2有交点P(x0,y0),则P∈C1,P∈C2即f1(x0,y0)=0,f2(x0,y0)=0 。所以x0,y0为方程组(1)的实数解。 (责任编辑:admin) |
