|
怎样分析教科书第99页上第13题的解题思路? 这道题是:过抛物线焦点的一条直线与它交于两点P,Q,通过点P和抛物线顶点的直线交准线于点M,求证直线MQ平行于抛物线的对称轴。 思路1:求出M,Q的纵坐标并进行比较,如果相等,则MQ∥x轴。为此,将方程  联立,解出 联立,解出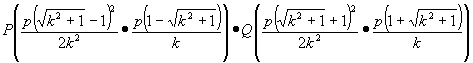 直线OP的方程为 直线OP的方程为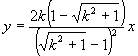 ,即 ,即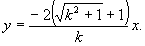 。令 。令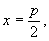 得M点纵坐标 得M点纵坐标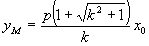 得正由此可见,按这一思路去证,运算较为烦琐。 得正由此可见,按这一思路去证,运算较为烦琐。思路2:利用教科书第99页上的第8题。即如果抛物线y2=2px的焦点的一条直线和这条抛物线相交,两个交点的纵坐标为y1,y2那么y1y2=-p2 。 设P(x1,y1),Q(x2,y2),M(x3,y3),并从y2=2px及 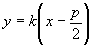 中消去x,得到ky2-2py-kp2=0,则有上述第8题结论y1y2=-p2 。即 中消去x,得到ky2-2py-kp2=0,则有上述第8题结论y1y2=-p2 。即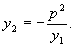 。 。又OP方程为 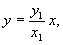 令 令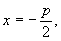 得 得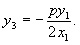 。 。因为P(x1,y1)抛物线上,所以 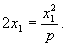 。 。从而  。 。这一证法运算量较小。 思路3:直线MQ的方程为y=y0的充要条件是 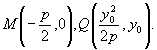 。 。将直线MO的方程 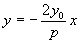 和直线QF的方程 和直线QF的方程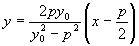 联立,它的解(x,y)就是点P的坐标,消去y0,可得y2=2px可知MQ的方程为y=y0的充要条件是点P在抛物线上,得证。 联立,它的解(x,y)就是点P的坐标,消去y0,可得y2=2px可知MQ的方程为y=y0的充要条件是点P在抛物线上,得证。这一证法巧用了充要条件来进行逆向思维,运用量也较小。 (责任编辑:admin) |
