|
题目:“用细绳拴着一个小球,使小球在光滑的水平面上做匀速圆周运动。”判断此过程中小球的机械能是否守恒。 机械能守恒定律的表述为:在一过程中若外力不做功,又每一对内非保守力不做功,则质点系机械能守恒,即 可见质点组机械能守恒的条件是: (1)外力不做功。因为外力做功将导致质点组(或系统)与外界进行能量交换; (2)每一对内非保守力不做功,或在该过程中的任意时间间隔内,每一对内非保守力所做功的代数和为零。 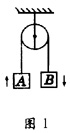 如图1所示,将不可伸长的轻绳、物体A,物体B和地球视为一质点组,设滑轮是理想的(即不计绳与滑轮、滑轮与轴承间的摩擦),又设悬挂两重物中其中之一的物体B质量较大,于是物体B加速下降,物体A加速上升。对于物体B而言,绳对物体B做负功,物体B对绳做正功,两者做功的代数和为零;对于物体A而言,绳对物体A做正功,物体A对绳做负功,两者做功的代数和为零,故质点组机械能守恒。 下面笔者从能的转化和功能关系角度来分析和理解机械能守恒的本质: 从能量转化角度看,只要在某一物理过程中。系统的机械能总量始终保持不变,而且系统内或系统与外界之间没有机械能转化为其他形式的能,也没有其他形式的能转化为系统的机械能,那么系统的机械能就是守恒的,与系统内是否一定发生动能和势能的相互转化无关。如在光滑的水平面上做匀速直线运动的物体。其机械能守恒;如果系统内或系统与外界之间有其他形式的能与机械能的转化。即使系统机械能总量保持不变,其机械能也是不守恒的,如在水平公路上以最大速度匀速行驶的汽车或在静止的海水中以最大速度匀速行驶的轮船,虽然机械能总量保持不变,但系统内有其他形式的能(内能或电能)转化为系统的机械能,系统又克服外界做功将机械能转化成其他形式的能。 从功能关系看,机械能守恒的条件是“系统外力不做功,系统内非保守力不做功”。这一条件与系统内保守力(重力或弹簧的弹力)是否做功无关,因为重力或弹簧弹力是否做功只是决定系统内是否发生动能和势能的相互转化,做功与否都不会改变系统机械能总量。 由此可知,如果质点组(系统)内各物体所受的所有力(包括重力和弹力)都不做功,则各物体的动能和势能均保持不变,动能和势能也不发生相互转化,此时质点组(或系统)的机械能也是守恒的。这是机械能守恒的特例。因此《教师教学用书》给出的上述习题答案是正确的。又如在水平面上光滑的圆形轨道上做匀速圆周运动的物体,虽然轨道对物体提供水平方向始终指向圆心的向心力作用,但对物体始终不做功,其机械能总量保持不变,故系统的机械能也是守恒的。 教材中机械能守恒定律的表述为:在只有重力做功的情形下,物体的动能和势能发生相互转化,但机械能总量保持不变。这是机械能守恒定律的最常见情形(即在重力势能和动能的相互转化中,只有重力做功的情况。实际上,在重力势能和弹性势能与动能的相互转化中,只有重力和弹簧的弹力做功时,物体的动能和系统的势能之和保持不变,系统的机械能守恒),也是更普遍的能量守恒定律的一种特殊情况。只是为了降低学生学习机械能守恒定律的难度。学习和掌握机械能守恒的条件一定要从能量转化和功能原理的角度来理解,这样更能体现机械能守恒条件的本质。 (责任编辑:admin) |
