|
辽河油田第三高级中学 杨闯 【本讲主要内容】 抛物线的定义及相关概念、抛物线的标准方程、抛物线的几何性质 【知识掌握】 【知识点精析】 1. 抛物线定义: 平面内与一个定点 2. 抛物线的标准方程有四种形式,参数 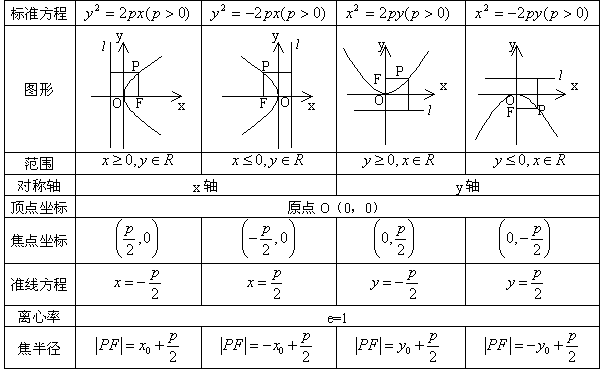 其中 3. 对于抛物线 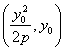 ,以简化运算。 ,以简化运算。4. 抛物线的焦点弦:设过抛物线 说明: 1. 求抛物线方程时,若由已知条件可知曲线是抛物线一般用待定系数法;若由已知条件可知曲线的动点的规律一般用轨迹法。 2. 凡涉及抛物线的弦长、弦的中点、弦的斜率问题时要注意利用韦达定理,能避免求交点坐标的复杂运算。 3. 解决焦点弦问题时,抛物线的定义有广泛的应用,而且还应注意焦点弦的几何性质。 【解题方法指导】 例1. 已知抛物线的顶点在坐标原点,对称轴为 解析:设所求抛物线的方程为 设交点 则 ∴点 ∴ 故所求抛物线方程为 例2. 设抛物线 解析:证法一:由题意知抛物线的焦点 故可设过焦点 由 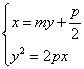 ,消去 ,消去设 ∵ ∴ 于是直线 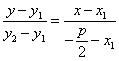 要证明  ,即证 ,即证注意到 证法二:同上得  ,知 ,知证法三:如图,  设 则 又根据抛物线的几何性质, ∴ 因此点 评述:本题考查抛物线的概念和性质,直线的方程和性质,运算能力和逻辑推理能力。其中证法一和二为代数法,证法三为几何法,充分运用了抛物线的几何性质,数形结合,更为巧妙。 【考点突破】 【考点指要】 抛物线部分是每年高考必考内容,考点中要求掌握抛物线的定义、标准方程以及几何性质,多出现在选择题和填空题中,主要考查基础知识、基础技能、基本方法,分值大约是5分。 考查通常分为四个层次: 层次一:考查抛物线定义的应用; 层次二:考查抛物线标准方程的求法; 层次三:考查抛物线的几何性质的应用; 层次四:考查抛物线与平面向量等知识的综合问题。 解决问题的基本方法和途径:待定系数法、轨迹方程法、数形结合法、分类讨论法、等价转化法。 【典型例题分析】 例3. (2006江西)设 A. C. 答案:B 解析:解法一:设点 解得 解法二:由题意设 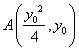 ,则 ,则 , ,即 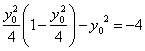 , ,评述:本题考查了抛物线的动点与向量运算问题。 例4. (2006安徽)若抛物线 A. -2 B. 2 C. -4 D. 4 答案:D 解析:椭圆 评述:本题考查抛物线与椭圆的标准方程中的基本量的关系。 【达标测试】 一. 选择题: 1. 抛物线 A. 2. 设抛物线的顶点在原点,其焦点在 A. 4 B. 4或-4 C. -2 D. -2或2 3. 焦点在直线 A. C. 4. 圆心在抛物线 A. C. 5. 正方体  A. 抛物线 B. 双曲线 C. 直线 D. 以上都不对 6. 已知点 A. 5 B. 4 C. 7. 已知点 A. 8. 过抛物线 A. 12 B. -12 C. 3 D. -3 二. 填空题: 9. 已知圆 10. 已知 11. 过点(0,1)的直线与 12. 已知直线 三. 解答题: 13. 已知抛物线顶点在原点,对称轴为 14. 过点 15. 设点F(1,0),M点在 ⑴当点 ⑵设 【综合测试】 一. 选择题: 1. (2005上海)过抛物线 A. 有且仅有一条 B. 有且仅有两条 C. 有无穷多条 D. 不存在 2. (2005江苏)抛物线 A. 3. (2005辽宁)已知双曲线的中心在原点,离心率为 A. 4. (2005全国Ⅰ)已知双曲线 A. 5. (2004全国)设抛物线 A. 6. (2006山东)动点 A. 7. (2004北京)在一只杯子的轴截面中,杯子内壁的曲线满足抛物线方程 A. 8. (2005北京)设抛物线 A. 8 B. 7 C. 10 D. 12 二. 填空题: 9. (2004全国Ⅳ)设  10. (2005北京)过抛物线 11. (2005辽宁)已知抛物线 12. (2004黄冈)已知抛物线 三. 解答题: 13. (2004山东)已知抛物线C: ⑴若以弦 ⑵在⑴的条件下,若 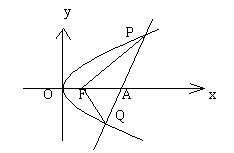 14. (2005四川) 如图, ⑴求抛物线方程; ⑵若 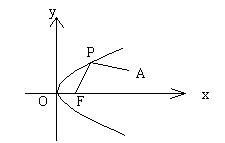 15. (2005河南)已知抛物线 ⑴求 ⑵求满足 (责任编辑:admin) |
