|
西城教育研修学院中学数学室供稿 班级 姓名 __ 学号 成绩________ 试卷I(本试卷共17小题,共100分) 一、选择题:(本大题共8小题,每小题5分,共40分) 1、已知 A. 2、设集合 A. 3、已知集合A到B的映射f:x→y = 2x + 1,那么集合A中元素2在B中的象是 A. 2 B. 5 C. 6 D. 8 ( ) 4、下列函数中,在区间(0,+∞)上是减函数的是( ) A. y = x2-1 .B. y = x3 C. y = -3x+2 D. y = log2x 5、已知 A. a +2b ..B. 6、已知定义在R上的函数f (x) 的图象是连续不断的,且有如下对应值表:
那么函数f (x) 一定存在零点的区间是( ) A. (-∞,1) ..B. (1,2) .C. (2,3) ..D. (3,+∞) 7、设 A.a<b<c B.a<c<b C.b<c<a D.c< a<b 8、函数y=ax+1的图象与函数y=loga(x+1)(其中a>0,且a≠1)的图象关于( ) A.直线y=x对称 B.直线y=x-1对称 C.直线y=x+1对称 D.直线y=-x+1对称 二、填空题:(本大题共6小题,每小题5分,共30分) 9、1.52.3与1.53.2的大小关系是1.52.3 1.53.2 (用“<” 或“>”表示). 10、函数y= 11、已知函数f(x)的定义域为[2,3],则函数f(x2)的定义域为____________. 12、计算log22+log51- 13、如果常数项为0的二次函数f (x) 的图象通过点M (1,5),N (-1,-3),那么这个函数的解析式为 . 14、设 三、解答题:(本大题共三小题,每题10分,共30分) 15、已知全集U={1,2,3,4,5,6,7,8},A={3,4,5},B={4,7,8}, ① 求出集合A的全部子集; ② 计算 16、已知二次函数 有等根, ①求f(x)的解析式; ②求函数 17、某工厂今年1月、 2月、3月生产某产品的数量分别为1万件、 1.2万件、 1.3万件,为了估测以后每个月的产量,以这三个月的产量数量为依据,用一个函数模拟该产品的月产量y与月份x的关系. 模拟函数可以选用二次函数或函数 试卷II 本试卷共7道小题,18—21题每小题5分,共50分 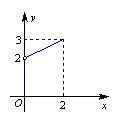 18、函数 18、函数19、已知f (x) 是定义在 时,f (x) 的图象如右图所示,那么f (x) 的值域 是 . 20、函数 21、定义在R上的函数 以下三道题为解答题 22、已知集合P={x|a+1≤x≤2a+1},Q={x|x2-3x≤0}, ⑴若a=3,求( 23、函数 ⑴求实数 ⑵用定义证明 ⑶写出 值或最小值.(本小问不需说明理由) 24、设S为满足下列两个条件的实数所构成的集合:①1 求解下列问题: ⑴若2∈S,此时集合S的元素最少是多少个,写出这个集合; ⑵S中所含元素个数一定是3n(n ∈N*)个吗?若是,请给出证明;若不是,试说明理由. 答案:试卷一 一、 选择题: ADBCDCAC 二、 填空题: 9、<; 10、(-∞,0); 11、[- 13、f(x)=x2+4x; 14、 三、解答题 15、⑴ ⑵ 16、⑴f(x)=- ⑵单增区间为[1,+∞) 单减区间为(-∞,0] 17、二次函数为y=-0.05x2+0.35x+1.4 当x=4时,y=1.30 另个一个函数y=0.8( 当x=4时,y=1.35 所以第二个函数较好 试卷二 18、一 ; 19、[-3,-2)∪(2,3]; 20、 22、⑴( ⑵a≤1 23、⑴a=1,b=0 f(x)= ⑶单减区间为(-∞,-1]和[1,+∞),最大值为 24、⑴最少3个,{2,-1, ⑵一定是3n个 161中第一模块考试题.zip (责任编辑:admin) |
