|
海南省教育研究培训院 罗才忠 教育部依照《普通高中数学课程标准(实验)》(以下简称《标准》)，为率先实施高中数学新课程实验的广东、山东、宁夏、海南四省(自治区)制定了《2007年普通高等学校招生全国统一考试数学考试考纲(课程标准实验版)》(以下简称《考纲》)．由于四省(自治区)学情不尽相同，他们各自制定了《2007年普通高等学校招生全国统一考试数学考试考纲(课程标准实验版)的说明》(以下简称说明》)．四省(自治区)的僦明》大同小异，宁夏和海南完全相同． 一、《说明》是高考命题的唯一依据 1．《说明》中“了解、理解、掌握”的含义 欲掌握各省的《说明》，首先要清楚《说明》中的“了解、理解、掌握”三个层次要求的含义． (1)了解．要求对所列知识的含义有初步的、感性的认识，知道这一知识内容是什么，按照一定的程序和步骤照样模仿，并能(或会)在有关的问题中识别和认识它． 这一层次涉及的主要行为动词有：了解，知道、识别、模仿，会求、会解等． (2)理解．要求对所列知识内容有较深刻的理性认识，知道知识间的逻辑关 系，能够对所列知识作正确的描述说明并用数学语言表达，能够利用所学的知识内容对相关问题进行比较、判别、讨论，具备利用所学知识解决简单问题的能力． 这一层次涉及的主要行为动词有：描述，说明，表达，推测、想象，比较、判别，初步运用等． (3)掌握．要求能够对所列知识内容进行推导证明，能够利用所学知识对问题进行分析、研究、讨论，并且加以解决．这一层次涉及的主要行为动词有：掌握、导出、分析，推导、证明，研究、讨论、运用、解决问题． 2．《标准》、《考纲》、《说明》之间的关系 各部分知识的整体要求与定位参照《标准》相应模块的有关说明，依照《考纲》而制定．《标准》、《考纲》、《说明》之问的关系如图1所示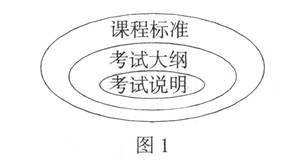．  3．《说明》的考试范围 课程改革经历了从“一纲一本”到“一标多本”的转变，根据《际准》编写的教材各有千秋，社会上高考复习资料五花八门，要在色彩斑斓的繁杂表象中认清形势，把握好各自省(自治区)的《说明》，就必须把握《说明》的考试范围． 新课程中增加的考试内容是比较好掌握的，关键是有些传统内容在《说明》中有较大的变化．例如，集合从传统教材的12课时缩减到新教材4课时，只要求掌握元素与集合、集合与集合之间的关系，集合的交、并、补运算．把集合与复数比较一下，同样都是4课时，由于集合知识在后续知识块中有着广泛的应用，因此集合比复数的地位重要，高考试题中没有复数题是可以的，但没有集合题是绝对不可以的． 新课程高考对立体几何的要求相对较低(宁夏、海南2007年新课程高考对二面角不作要求，从而降低了立体几何的难度)，文理科的区别在于文科考生没有学习空间向量，仅在必修3里用了18课时来学习立体几何初步，这一模块对推理论证要求较低． 新课程高考中，概率部分在文理科要求上有一些区别．理科增加了条件概率与几何概型，概率分布仅要求涉及取有限个值的随机变量．文科在概率部分仅保留了互斥事件的概率加法公式，增加了几何概型． 新课程高考中，解析几何在文理科要求上的区别是理科对双曲线作为“了解”要求，文科对抛物线、双曲线作为“了解”要求． 特别要指出的是数列知识块中只要求掌握等差数列通项、等比数列通项、求和公式及其简单应用． 二、新课程的主干知识块 高考大题离不开主干知识块的支撑．传统的六大块包括：基本初等函数I(指数函数、对数函数、幂函数)，基本初等函数Ⅱ(三角函数)、三角恒等变换与解三角形，立体几何，平面解析几何，数列，不等式．这些还是新课程的主干知识块吗?欲回答此问题，我们先看看《说明》中各知识块的教学课时统计． 表1：理科必考部分
表2：理科选考部分
表3：文科必考部分
表4：文科选考部分
根据上表分析，基本初等函数I(指数函数、对数函数、幂函数)，基本初等函数Ⅱ(三角函数)、三角恒等变换与解三角形，立体几何与空间向量，平面解析几何，概率统计及其案例，是新课程中的五大主干知识块．数列与不等式已被削弱，数列与不等式比较，数列地位较不等式弱．当然，如果把选修系列4中的“不等式选讲”作为必考内容，那不等式也是主干知识块．有必要说明的是，文科立体几何虽然只有18课时，但由于其地位的重要性，文科的立体几何也应该作为主干知识块，即文科的立体几何大题是不可缺少的． 三、关注高考改革的连续性和稳定性 2007年的新课程高考试题仍会保持高考改革的连续性和稳定性，坚持以能力立意命题，突出考能力与数学素质是命题的方向，为了“有利于中学数学教学，有利于高校选拔”，将重视对教材内容的考查．加大思维量，适当减少运算量，降低人手难度，考查主干知识和通性通法，重视考查逻辑思维能力，运算能力，空间想象能力，分析问题和解决实际问题的能力和创新意识，强调探究性、综合性和开放性． 选择题和填空题考查的方向仍是知识的广度和解题的速度，考查逻辑思维能力、直觉思维能力和对概念的理解辨析能力，“概念是否模糊不清，方法是否模棱两可”是考生必须解决的问题．另外，选择题和填空题一直是新题型的试验田，往年试验成功的“多选题”和“开放性试题”的题型都是在这里出现的，但新题型不会是难题，只要认真分析、联想、转化，沉着应答即可解决． 解答题命题仍从能力立意，考查数学思想方法、倡导理性思维的基本指导思想，考查考生潜能为基本命题思路，加大对新增知识考查的力度．将新旧知识综合的基本精神不会变．三角函数大题要联系基本公式、基本定理的应用．立体几何综合大题仍将可能有两种解法：常规解法(综合法)；利用空间向量(坐标)求解(证明)．概率大题是概率统计或与生产、生活实际联系的数学建模题．函数综合题(可以是函数与数列、函数与不等式，函数与导数)，要注意用导数来研究函数的性质和题型解法的总结．解析几何综合题要注意与平面向量知识的结合． 四、考前模拟试题的编制 考前模拟试题的编制得体对学生应考能起到良好的导向作用．5月份只需编制3套试卷便基本可以覆盖《说明》的逐个要求．所有试题都必须改编或创作，拒绝成题，反对陈题． 考前模拟试题的编制要依靠高三备课组集体的力量，切忌单打独斗，单打独斗容易导致以偏概全．另外，难度适中也非常重要．命题者知道，试题太难或太简单都没有区分度． 选择题和填空题的准备，10个必考模块中的每个知识块准备2个符合难度要的选择题或填空题．例如，必修4有“三角函数的性质、平面向量、三角恒等变换”三个知识块．这样就有五六十个选择题和填空题备用． 文、理科数学按照主干知识块设计大题．设计的大题要有区分度，前面两个大题要面向中等考生，让他们看到希望．像例1这样的试题，能够让中等考生看到希望． 例1如图2, 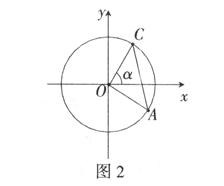 与x轴的正半轴的交点为A，点C和点B在上，且点C位于第一象限，点B的坐标为 . (1)求 的半径的长及用 的三角函数表示点C的坐标；(2)若  ,求tan的值．这样的试题简单而涉及知识点多，入手容易，解法多样，有一定的区分度． 三角函数作为基础大题应该是特定的，三套题中，要分别涉及三角函数的性质、三角恒等变换和解三角形． 设计大题时要注意和十几学时的综合，但综合时要分清主次．例如，函数和数列综合时，函数为主，数列为次，数列只局限于等差数列的通项、等比数列的通项与求和公式的运用． 下面是函数与导数、函数与数列、函数与不等式的综合试题． 例2已知函数  (1)求a、b的值； (2)对任意  、 不等式 ≤m恒成立，试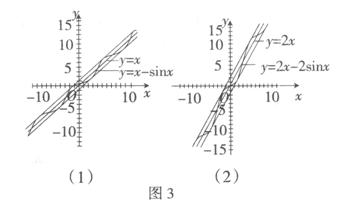求实数m的取值范围；(3)设直线  曲线 ．若直线l与曲线S同时满足下列两个条件：直线l与曲线S相切且至少有两个切点；对任意 都有 ，则称直线l为曲线S的“上夹线”．观察图3：  根据图3，试推测曲线  的“上夹线”的方程，并作适当的说明．例3已知函数  ．(1)判断点  是否在函数的图象上?(2)求f(x)>0的解集； (3)记数列  的通项公式为 ， 求数列的前n项和 ．例4已知函数  。 (1)证明：  对定义域内的所有x都成立；(2)当  的定义域为 时，求证： ;(3)设函数  求g(X)的最小值．解析几何试题设计时理科分别以椭圆、抛物线、轨迹问题为背景，文科两个题以椭圆为背景，一个题以轨迹为背景．文、理科的解析几何都要联系直线与圆锥曲线的位置关系及其基本公式的运用． 以下是三道解析几何例题． 例5已知椭圆 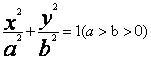 的右顶点为A，0为坐标原点，M为椭圆上一点，且 ．(1)若  ，试求椭圆的离心率；(2)若椭圆的离心率为  ，且 ，试求椭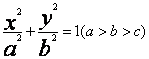圆的方程．例6椭圆  长轴的左端点A(2，O)，点 是椭圆的右焦点，点 ．(1)求椭圆的方程； (2)过原点O的直线交椭圆于点B和点C，求△BCM面积的最大值． 例7 已知点H(一3，0)，点P在y轴上，点Q在x轴的正半轴上，点M在直线PQ，且满足  , ．(1)当点P在y轴上移动时，求点M的轨迹C的方程； (2)设点F(1，0)，A是轨迹C上横坐标为4、且位于x轴上方的点．过A作AB垂直于y轴，垂足为B，OB的中点为M以M为圆心，MB为半径作圆M，当K(m，0)是x轴上一动点时，讨论直线AK与圆M的位置关系． 有必要说明的是文科用例7应试并没超出《考纲》的范围，虽然抛物线的知识目标是“了解”，但解出抛物线的过程所用的知识仍然是要求“理解”与“掌握”的． (责任编辑：admin) |