37.(辽宁•理•18题)如图,在直三棱柱 中, 中,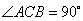 , , , ,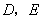 分别为棱 分别为棱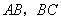 的中点, 的中点,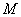 为棱 为棱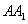 上的点,二面角 上的点,二面角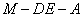 为 为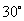 。 。
(I)证明: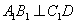 ; ;
(II)求 的长,并求点 的长,并求点 到平面 到平面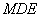 的距离。 的距离。

【解答】本小题主要考查空间中的线面关系,解三角形等基础知识,考查空间想象能力与思维能力
(I)证明:连结 , ,
三棱柱 是直三棱柱, 是直三棱柱,
 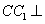 平面 平面 , ,
  为 为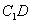 在平面 在平面 内的射影. 内的射影.
 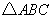 中, 中,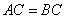 , , 为 为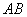 中点, 中点,
  , ,
  . .
  , ,
 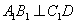 .············ 4分 .············ 4分
(II)解法一:过点 作 作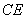 的平行线,交 的平行线,交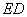 的延长线于 的延长线于 ,连结 ,连结 . .
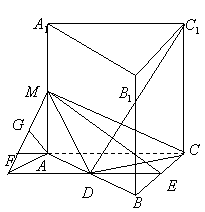
 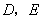 分别为 分别为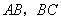 的中点, 的中点,
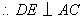 . .
又  , ,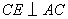 . .
 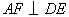 . .
  平面 平面 , ,
 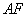 为 为 在平面 在平面 内的射影. 内的射影.
  . .
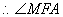 为二面角 为二面角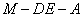 的平面角, 的平面角, . .
在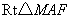 中, 中,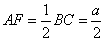 , , , ,
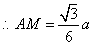 . .
作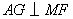 ,垂足为 ,垂足为 , ,
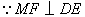 , ,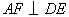 , ,
  平面 平面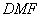 , ,
 平面 平面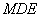 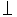 平面 平面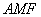 , ,
 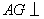 平面 平面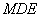 . .
在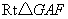 中, 中,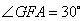 , ,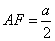 , ,
  ,即 ,即 到平面 到平面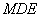 的距离为 的距离为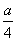 . .
  , ,
 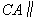 平面 平面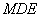 , ,
  到平面 到平面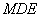 的距离与 的距离与 到平面 到平面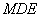 的距离相等,为 的距离相等,为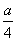 . .
解法二:过点 作 作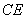 的平行线,交 的平行线,交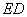 的延长线于 的延长线于 ,连接 ,连接 . .
 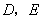 分别为 分别为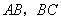 的中点, 的中点,
 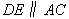 . .
又  , ,
 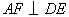 . .
  平面 平面 , ,
 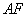 是 是 在平面 在平面 内的射影, 内的射影,
  . .
 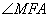 为二面角 为二面角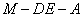 的平面角, 的平面角, . .
在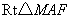 中, 中,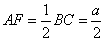 , , , ,
  .············· 8分 .············· 8分
设 到平面 到平面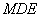 的距离为 的距离为 , ,
 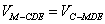 . .
 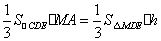
 , , , ,
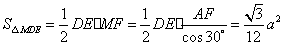 , ,
 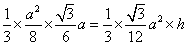 , ,
 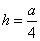 ,即 ,即 到平面 到平面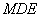 的距离为 的距离为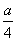 . 12分 . 12分
38.(宁夏•理•19题)如图,在三棱锥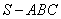 中,侧面 中,侧面 与侧面 与侧面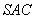 均为等边三角形, 均为等边三角形,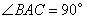 , , 为 为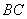 中点. 中点.
(Ⅰ)证明: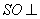 平面 平面 ;(Ⅱ)求二面角 ;(Ⅱ)求二面角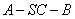 的余弦值. 的余弦值.
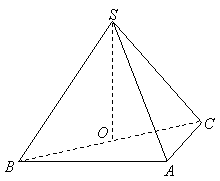 
【解答】(Ⅰ)证明:由题设  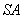 ,连结 ,连结 , ,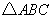 为等腰直角三角形,所以 为等腰直角三角形,所以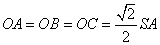 ,且 ,且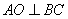 ,又 ,又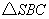 为等腰三角形,故 为等腰三角形,故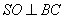 ,且 ,且 ,从而 ,从而 . .
所以 为直角三角形, 为直角三角形, . .
又 . .
所以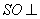 平面 平面 . .
(Ⅱ)解法一:
取 中点 中点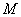 ,连结 ,连结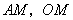 ,由(Ⅰ)知 ,由(Ⅰ)知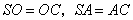 ,得 ,得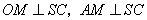 . .
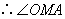 为二面角 为二面角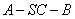 的平面角. 的平面角.
由 得 得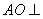 平面 平面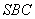 . .
所以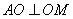 ,又 ,又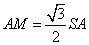 ,故 ,故 . .
所以二面角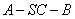 的余弦值为 的余弦值为 . .
解法二:以 为坐标原点,射线 为坐标原点,射线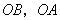 分别为 分别为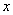 轴、 轴、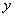 轴的正半轴,建立如图的空间直角坐标系 轴的正半轴,建立如图的空间直角坐标系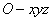 . .
 
设 ,则 ,则 . .
 的中点 的中点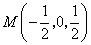 , , . .
 . .
故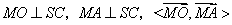 等于二面角 等于二面角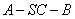 的平面角. 的平面角.
 , ,
所以二面角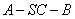 的余弦值为 的余弦值为 . .
39.(陕西•理•19题)如图,在底面为直角梯形的四棱锥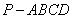 中 中 , ,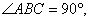 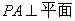  , ,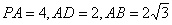 ,BC=6。 ,BC=6。
(Ⅰ)求证: ;(Ⅱ)求二面角 ;(Ⅱ)求二面角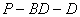 的大小; 的大小;

【解答】解法一:(Ⅰ) 平面 平面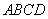 , , 平面 平面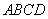 . . . .
又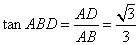 , ,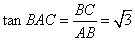 . .
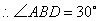 , , , ,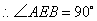 ,即 ,即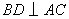 . .
又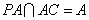 . . 平面 平面 . .
(Ⅱ)过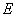 作 作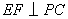 ,垂足为 ,垂足为 ,连接 ,连接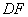 . .
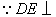 平面 平面 , ,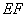 是 是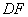 在平面 在平面 上的射影,由三垂线定理知 上的射影,由三垂线定理知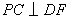 , ,
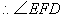 为二面角 为二面角 的平面角. 的平面角.
 
又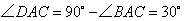 , ,
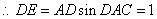 , ,
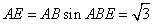 , ,
又 , ,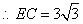 , , . .
由 得 得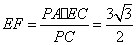 . .
在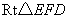 中, 中, , , . .
 二面角 二面角 的大小为 的大小为 . .
解法二:(Ⅰ)如图,建立坐标系,
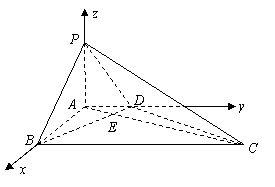 
则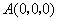 , , , ,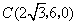 , ,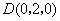 , ,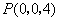 , ,
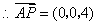 , ,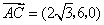 , , , ,
 , , . .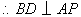 , ,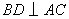 , ,
又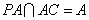 , , 平面 平面 . .
(Ⅱ)设平面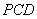 的法向量为 的法向量为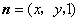 , ,
则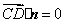 , ,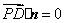 , ,
又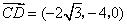 , , , ,
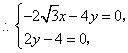 解得 解得
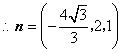
平面 的法向量取为 的法向量取为 , ,
 , , . .
 二面角 二面角 的大小为 的大小为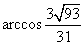 . .
(责任编辑:admin) |






 ,
,




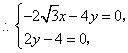 解得
解得
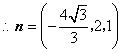
 .
.