|
34、(全国一文 20)设函数 (Ⅰ)求a、b的值; (Ⅱ)若对于任意的 【解答】(Ⅰ) 因为函数 即 解得 (Ⅱ)由(Ⅰ)可知, 当 当 当 所以,当 则当 因为对于任意的 所以 解得 因此 35、(全国二理 22)已知函数 (1)求曲线 (2)设 【解答】(1)求函数 曲线 即 (2)如果有一条切线过点 于是,若过点 有三个相异的实数根. 记 则 当
由 当 当 综上,如果过 即 36、(全国二文 22)已知函数 (1)证明 (2)若z=a+2b,求z的取值范围。 【解答】求函数 (Ⅰ)由函数 所以 当 (Ⅱ)在题设下, 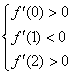 即 即 . .化简得 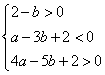 . .此不等式组表示的区域为平面 所围成的 所以 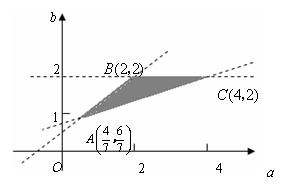  37、(山东理 22)设函数 (Ⅰ)当 (Ⅱ)求函数 (Ⅲ)证明对任意的正整数 【解答】(Ⅰ)由题意知, 设 当 即 (Ⅱ)①由(Ⅰ)得,当 ② 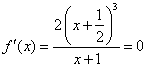 有两个相同的解 有两个相同的解③当 即
由此表可知: 当 此时,
由此表可知: 综上所述: (Ⅲ)当 令函数 则 又 故当 对任意正整数 所以结论成立. 38、(山东文 21)设函数 证明:当 【解答】因为 当 如果 所以当 当  令 将 当
从上表可看出, 函数 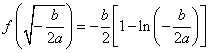 . .当
从上表可看出, 函数 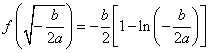 .综上所述, .综上所述,当 当 若 若 (责任编辑:admin) |


