|
53、(山东文17)在 解:(1) 又 解得 (2) 又 54、(陕西理17)设函数 解:(Ⅰ) 由已知 (Ⅱ)由(Ⅰ)得 由 55、(上海理17)在 解: 由题意,得 由正弦定理得 56、(四川理17)已知 本题考察三角恒等变形的主要基本公式、三角函数值的符号,已知三角函数值求角以及计算能力。 解:(Ⅰ)由 ∴  (Ⅱ)由 又∵ 由 所以 57、(天津理17)已知函数 本小题考查三角函数中的诱导公式、特殊角三角函数值、两角差公式、倍角公式、函数 (Ⅰ)解: 因此,函数 (Ⅱ)解法一:因为 故函数 解法二:作函数  由图象得函数 58、(天津文17)在 本小题考查同角三角函数的基本关系式、两角和公式、倍角公式、正弦定理等的知识,考查基本运算能力.满分12分. (Ⅰ)解:在  ,由正弦定理, ,由正弦定理,所以 (Ⅱ)解:因为  , ,59、(浙江理18)已知 解:(I)由题意及正弦定理,得 两式相减,得 (II)由 由余弦定理,得 所以 C浙江文2.已知 A. 60、(重庆理17)设 解:(Ⅰ) 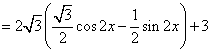 故 最小正周期 (Ⅱ)由 又由 从而 61、(重庆文18)已知函数  . .(Ⅰ)求 (Ⅱ)若角 解:(Ⅰ) 由 故 (Ⅱ)由已知条件得 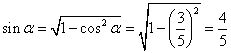 . .从而   (责任编辑:admin) |
