|
第一部分 选择题(共50分) 一、选择题:本大题共10小题,每小题5分,满分50分. 在每小题给出的四个选项中,有且只有一项是符合题目要求的.请将答案代号填在答题卷的相应位置上. 1.已知点A(-1,0)、B(1,3),向量 A.-2 B.-1 C.1 D.2 2.设 A. C. 3.已知圆 A.0或4 B.1或3 C.-2或6 D.-1或3 4.已知 A.命题“p且q”为真 B.命题“p或 C.命题“p或q”为假 D.命题“ 5.设 A. C. 6.椭圆 A. 7.已知函数 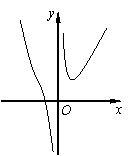 A. C. 8.设x,y满足约束条件  则 则A. 9.如图, 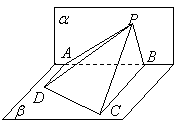 A.圆的一部分 B.椭圆的一部分 C.双曲线的一部分 D.抛物线的一部分 10.已知 A.4 第二部分 非选择题(共100分) 二、填空题:本大题共4小题,每小题5分,满分20分. 请将答案填在答题卷的相应位置上. 11.等差数列有如下性质:若 12.已知集合 13.在△ABC中,若 14.在四面体ABCD中,已知AB=CD=5,AC=BD=5,AD=BC=6.则四面体ABCD的体积为 ;四面体ABCD外接球的面积为 . 三、解答题:本大题共6小题,共80分.解答应写出文字说明、演算步骤或推证过程. 15.(本小题满分12分) 已知向量 (Ⅰ)求函数 (Ⅱ)求函数 16.(本小题满分12分) 箱中装有12张大小、重量一样的卡片,每张卡片正面分别标有1到12中的一个号码,正面号码为 (Ⅰ)如果任意取出一张卡片,试求正面数字不大于反面数字的概率; (Ⅱ)如果同时取出两张卡片,试求他们反面数字相同的概率. 17.(本小题满分14分) 如图,在矩形ABCD中,AB=2,BC=a,又PA⊥平面ABCD,PA=4. (Ⅰ)若在边BC上存在一点Q,使PQ⊥QD,求a的取值范围; (Ⅱ)当边BC上存在唯一点Q,使PQ⊥QD时,求二面角A-PD-Q的余弦值. 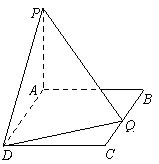  18.(本小题满分14分) 已知函数 (Ⅰ)求函数 (Ⅱ)若函数 19.(本小题满分14分) 已知点(x,y)在椭圆C: (Ⅰ)求点 (Ⅱ)若把轨迹 20.(本小题满分14分) 已知正项数列  . .(Ⅰ)求数列 (Ⅱ)定理:若函数 请根据上述定理,且已知函数 (Ⅲ)求证: 参考答案 一、选择题:本大题共10小题,每小题5分,满分50分. 1.B 2.A 3.D 4.C 5.D 6.C 7.A 8.D 9.B 10.C 二、填空题:本大题共4小题,每小题5分,满分20分. 第14题的第一个空2分,第二个空3分. 11. 三、解答题: 15. = = = (Ⅰ)当 函数 (Ⅱ)当 故函数 16.(Ⅰ)由不等式 由于 即共有9张卡片正面数字不大于反面数字, 故所求的概率为 答:正面数字不大于反面数字的概率为 (Ⅱ)设取出的是第 则有 即 故符合条件的取法为1,8;2,7;3,6;4,5. 故所求的概率为 答:反面数字相同的概率为 17.解法1:(Ⅰ)如图,连 ……2分 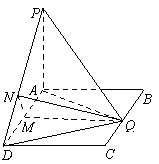  设 在 在 在 即 ∴ 故 (Ⅱ)由(Ⅰ)知,当 过Q作QM∥CD交AD于M,则QM⊥AD. ∵PA⊥平面ABCD,∴PA⊥QM.∴QM⊥平面PAD. 过M作MN⊥PD于N,连结NQ,则QN⊥PD. ∴∠MNQ是二面角A-PD-Q的平面角. ……10分 在等腰直角三角形 ∴ 故二面角A-PD-Q的余弦值为 解法2:(Ⅰ)以   B(0,2,0),C(a,2,0),D(a,0,0), P(0,0,4), ……2分 设Q(t,2,0)( ∵PQ⊥QD,∴ 即 ∴ 故 (Ⅱ)由(Ⅰ)知,当 此时Q(2,2,0),D(4,0,0). ……8分 设 由 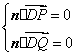 ,得 ,得取 而 由 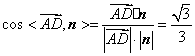 . .∴二面角A-PD-Q的余弦值为 18.当 令 且 (Ⅰ)当 当
……8分 ∴ 当 (Ⅱ)要使函数 必须 解得 ∴当 19.(Ⅰ)设点( 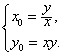 ……2分 ……2分∴ ∵点(x,y)在椭圆C: ∴ 故所求的轨迹 (Ⅱ)由轨迹 ∴  . .所以,当且仅当 如果在开区间 此时, ∴椭圆C的离心率的取值范围是 20.(Ⅰ) 由于 当 整理,得 由于 ∴数列 从而 ∴ (Ⅱ)由(Ⅰ)知 对于 根据定理,得 整理,得 令 ∴  . .∴ (Ⅲ)∵ ∴ 又由(Ⅱ),得 (或 ∴ (责任编辑:admin) |
