湖南省常德市安乡县第五中学 龚光勇收集整理
1.圆锥曲线的两个定义:
(1)第一定义中要重视“括号”内的限制条件:椭圆中,与两个定点F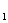 ,F ,F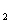 的距离的和等于常数 的距离的和等于常数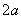 ,且此常数 ,且此常数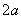 一定要大于 一定要大于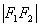 ,当常数等于 ,当常数等于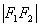 时,轨迹是线段F 时,轨迹是线段F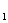 F F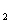 ,当常数小于 ,当常数小于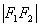 时,无轨迹;双曲线中,与两定点F 时,无轨迹;双曲线中,与两定点F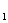 ,F ,F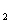 的距离的差的绝对值等于常数 的距离的差的绝对值等于常数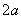 ,且此常数 ,且此常数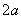 一定要小于|F 一定要小于|F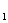 F F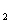 |,定义中的“绝对值”与 |,定义中的“绝对值”与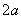 <|F <|F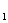 F F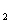 |不可忽视。若 |不可忽视。若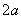 =|F =|F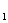 F F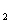 |,则轨迹是以F |,则轨迹是以F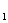 ,F ,F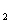 为端点的两条射线,若 为端点的两条射线,若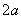 ﹥|F ﹥|F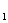 F F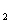 |,则轨迹不存在。若去掉定义中的绝对值则轨迹仅表示双曲线的一支。比如: |,则轨迹不存在。若去掉定义中的绝对值则轨迹仅表示双曲线的一支。比如:
①已知定点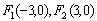 ,在满足下列条件的平面上动点P的轨迹中是椭圆的是 ,在满足下列条件的平面上动点P的轨迹中是椭圆的是
A.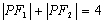 B. B.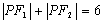
C.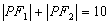 D. D.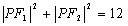 (答:C); (答:C);
②方程 表示的曲线是_____(答:双曲线的左支) 表示的曲线是_____(答:双曲线的左支)
(2)第二定义中要注意定点和定直线是相应的焦点和准线,且“点点距为分子、点线距为分母”,其商即是离心率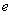 。圆锥曲线的第二定义,给出了圆锥曲线上的点到焦点距离与此点到相应准线距离间的关系,要善于运用第二定义对它们进行相互转化。 。圆锥曲线的第二定义,给出了圆锥曲线上的点到焦点距离与此点到相应准线距离间的关系,要善于运用第二定义对它们进行相互转化。
如已知点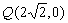 及抛物线 及抛物线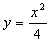 上一动点P(x,y),则y+|PQ|的最小值是_____(答:2) 上一动点P(x,y),则y+|PQ|的最小值是_____(答:2)
2.圆锥曲线的标准方程(标准方程是指中心(顶点)在原点,坐标轴为对称轴时的标准位置的方程):
(1)椭圆:焦点在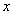 轴上时 轴上时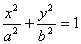 ( (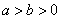 ) )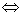 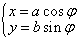 (参数方程,其中 (参数方程,其中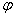 为参数),焦点在 为参数),焦点在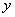 轴上时 轴上时 =1( =1(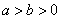 )。方程 )。方程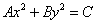 表示椭圆的充要条件是什么?(ABC≠0,且A,B,C同号,A≠B)。比如: 表示椭圆的充要条件是什么?(ABC≠0,且A,B,C同号,A≠B)。比如:
①已知方程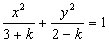 表示椭圆,则 表示椭圆,则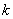 的取值范围为____(答: 的取值范围为____(答: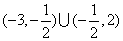 ); );
②若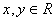 ,且 ,且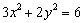 ,则 ,则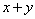 的最大值是____, 的最大值是____,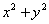 的最小值是___(答: 的最小值是___(答: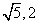 ) )
(2)双曲线:焦点在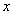 轴上: 轴上: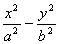 =1,焦点在 =1,焦点在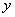 轴上: 轴上: =1( =1(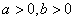 )。方程 )。方程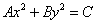 表示双曲线的充要条件是什么?(ABC≠0,且A,B异号)。比如: 表示双曲线的充要条件是什么?(ABC≠0,且A,B异号)。比如:
①双曲线的离心率等于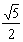 ,且与椭圆 ,且与椭圆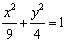 有公共焦点,则该双曲线的方程_______(答: 有公共焦点,则该双曲线的方程_______(答: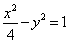 ); );
②设中心在坐标原点 ,焦点 ,焦点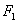 、 、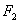 在坐标轴上,离心率 在坐标轴上,离心率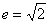 的双曲线C过点 的双曲线C过点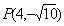 ,则C的方程为_______(答: ,则C的方程为_______(答: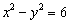 ) )
(3)抛物线:开口向右时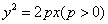 ,开口向左时 ,开口向左时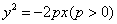 ,开口向上时 ,开口向上时 ,开口向下时 ,开口向下时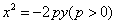 。 。
3.圆锥曲线焦点位置的判断(首先化成标准方程,然后再判断):
(1)椭圆:由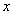 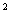 , ,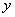 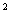 分母的大小决定,焦点在分母大的坐标轴上。 分母的大小决定,焦点在分母大的坐标轴上。
如已知方程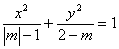 表示焦点在y轴上的椭圆,则m的取值范围是__(答: 表示焦点在y轴上的椭圆,则m的取值范围是__(答: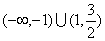 ) )
(2)双曲线:由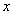 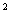 , ,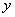  项系数的正负决定,焦点在系数为正的坐标轴上; 项系数的正负决定,焦点在系数为正的坐标轴上;
(3)抛物线:焦点在一次项的坐标轴上,一次项的符号决定开口方向。
特别提醒:(1)在求解椭圆、双曲线问题时,首先要判断焦点位置,焦点F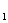 ,F ,F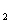 的位置,是椭圆、双曲线的定位条件,它决定椭圆、双曲线标准方程的类型,而方程中的两个参数 的位置,是椭圆、双曲线的定位条件,它决定椭圆、双曲线标准方程的类型,而方程中的两个参数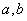 ,确定椭圆、双曲线的形状和大小,是椭圆、双曲线的定形条件;在求解抛物线问题时,首先要判断开口方向;(2)在椭圆中, ,确定椭圆、双曲线的形状和大小,是椭圆、双曲线的定形条件;在求解抛物线问题时,首先要判断开口方向;(2)在椭圆中,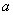 最大, 最大,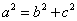 ,在双曲线中, ,在双曲线中,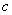 最大, 最大,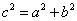 。 。
4.圆锥曲线的几何性质:
(1)椭圆(以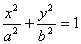 ( (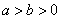 )为例):①范围: )为例):①范围: ;②焦点:两个焦点 ;②焦点:两个焦点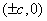 ;③对称性:两条对称轴 ;③对称性:两条对称轴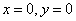 ,一个对称中心(0,0),四个顶点 ,一个对称中心(0,0),四个顶点 ,其中长轴长为2 ,其中长轴长为2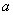 ,短轴长为2 ,短轴长为2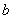 ;④准线:两条准线 ;④准线:两条准线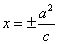 ; ⑤离心率: ; ⑤离心率: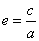 ,椭圆 ,椭圆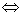 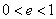 , ,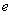 越小,椭圆越圆; 越小,椭圆越圆;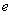 越大,椭圆越扁。比如: 越大,椭圆越扁。比如:
①若椭圆 的离心率 的离心率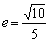 ,则 ,则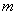 的值是__(答:3或 的值是__(答:3或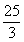 ); );
②以椭圆上一点和椭圆两焦点为顶点的三角形的面积最大值为1时,则椭圆长轴的最小值为__(答: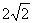 ) )
(2)双曲线(以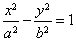 ( (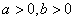 )为例):①范围: )为例):①范围: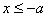 或 或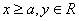 ;②焦点:两个焦点 ;②焦点:两个焦点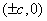 ;③对称性:两条对称轴 ;③对称性:两条对称轴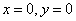 ,一个对称中心(0,0),两个顶点 ,一个对称中心(0,0),两个顶点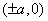 ,其中实轴长为2 ,其中实轴长为2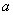 ,虚轴长为2 ,虚轴长为2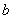 ,特别地,当实轴和虚轴的长相等时,称为等轴双曲线,其方程可设为 ,特别地,当实轴和虚轴的长相等时,称为等轴双曲线,其方程可设为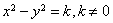 ;④准线:两条准线 ;④准线:两条准线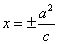 ; ⑤离心率: ; ⑤离心率: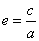 ,双曲线 ,双曲线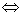 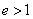 ,等轴双曲线 ,等轴双曲线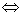 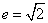 , ,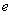 越小,开口越小, 越小,开口越小,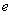 越大,开口越大;⑥两条渐近线: 越大,开口越大;⑥两条渐近线: 。比如: 。比如:
①双曲线的渐近线方程是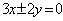 ,则该双曲线的离心率等于______(答: ,则该双曲线的离心率等于______(答: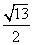 或 或 ); );
②双曲线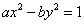 的离心率为 的离心率为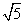 ,则 ,则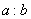 = (答:4或 = (答:4或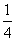 ); );
③设双曲线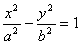 (a>0,b>0)中,离心率e∈[ (a>0,b>0)中,离心率e∈[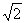 ,2],则两条渐近线夹角θ的取值范围是________(答: ,2],则两条渐近线夹角θ的取值范围是________(答: ); );
(3)抛物线(以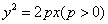 为例):①范围: 为例):①范围: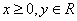 ;②焦点:一个焦点 ;②焦点:一个焦点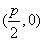 ,其中 ,其中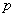 的几何意义是:焦点到准线的距离;③对称性:一条对称轴 的几何意义是:焦点到准线的距离;③对称性:一条对称轴 ,没有对称中心,只有一个顶点(0,0);④准线:一条准线 ,没有对称中心,只有一个顶点(0,0);④准线:一条准线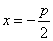 ; ⑤离心率: ; ⑤离心率: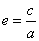 ,抛物线 ,抛物线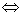 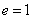 。 。
如设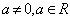 ,则抛物线 ,则抛物线 的焦点坐标为________(答: 的焦点坐标为________(答: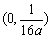 ); );
5、点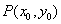 和椭圆 和椭圆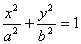 ( (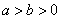 )的关系:(1)点 )的关系:(1)点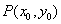 在椭圆外 在椭圆外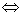  ;(2)点 ;(2)点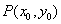 在椭圆上 在椭圆上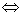 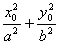 =1;(3)点 =1;(3)点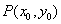 在椭圆内 在椭圆内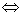 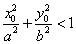
6.直线与圆锥曲线的位置关系:
(1)相交: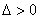 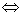 直线与椭圆相交; 直线与椭圆相交; 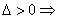 直线与双曲线相交,但直线与双曲线相交不一定有 直线与双曲线相交,但直线与双曲线相交不一定有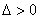 ,当直线与双曲线的渐近线平行时,直线与双曲线相交且只有一个交点,故 ,当直线与双曲线的渐近线平行时,直线与双曲线相交且只有一个交点,故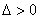 是直线与双曲线相交的充分条件,但不是必要条件; 是直线与双曲线相交的充分条件,但不是必要条件;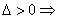 直线与抛物线相交,但直线与抛物线相交不一定有 直线与抛物线相交,但直线与抛物线相交不一定有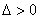 ,当直线与抛物线的对称轴平行时,直线与抛物线相交且只有一个交点,故 ,当直线与抛物线的对称轴平行时,直线与抛物线相交且只有一个交点,故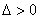 也仅是直线与抛物线相交的充分条件,但不是必要条件。比如: 也仅是直线与抛物线相交的充分条件,但不是必要条件。比如:
①若直线y=kx+2与双曲线x2-y2=6的右支有两个不同的交点,则k的取值范围是_______(答:(-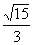 ,-1)); ,-1));
②直线y―kx―1=0与椭圆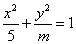 恒有公共点,则m的取值范围是_______(答:[1,5)∪(5,+∞)); 恒有公共点,则m的取值范围是_______(答:[1,5)∪(5,+∞));
③过双曲线 的右焦点直线交双曲线于A、B两点,若│AB︱=4,则这样的直线有_____条(答:3); 的右焦点直线交双曲线于A、B两点,若│AB︱=4,则这样的直线有_____条(答:3);
(2)相切: 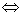 直线与椭圆相切; 直线与椭圆相切; 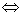 直线与双曲线相切; 直线与双曲线相切; 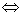 直线与抛物线相切; 直线与抛物线相切;
(3)相离: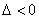 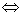 直线与椭圆相离; 直线与椭圆相离;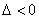 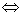 直线与双曲线相离; 直线与双曲线相离;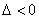 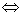 直线与抛物线相离。 直线与抛物线相离。
特别提醒:
(1)直线与双曲线、抛物线只有一个公共点时的位置关系有两种情形:相切和相交。如果直线与双曲线的渐近线平行时,直线与双曲线相交,但只有一个交点;如果直线与抛物线的轴平行时,直线与抛物线相交,也只有一个交点;
(2)过双曲线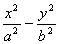 =1外一点 =1外一点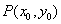 的直线与双曲线只有一个公共点的情况如下:①P点在两条渐近线之间且不含双曲线的区域内时,有两条与渐近线平行的直线和分别与双曲线两支相切的两条切线,共四条;②P点在两条渐近线之间且包含双曲线的区域内时,有两条与渐近线平行的直线和只与双曲线一支相切的两条切线,共四条;③P在两条渐近线上但非原点,只有两条:一条是与另一渐近线平行的直线,一条是切线;④P为原点时不存在这样的直线; 的直线与双曲线只有一个公共点的情况如下:①P点在两条渐近线之间且不含双曲线的区域内时,有两条与渐近线平行的直线和分别与双曲线两支相切的两条切线,共四条;②P点在两条渐近线之间且包含双曲线的区域内时,有两条与渐近线平行的直线和只与双曲线一支相切的两条切线,共四条;③P在两条渐近线上但非原点,只有两条:一条是与另一渐近线平行的直线,一条是切线;④P为原点时不存在这样的直线;
(3)过抛物线外一点总有三条直线和抛物线有且只有一个公共点:两条切线和一条平行于对称轴的直线。比如:
①过点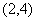 作直线与抛物线 作直线与抛物线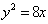 只有一个公共点,这样的直线有______(答:2); 只有一个公共点,这样的直线有______(答:2);
②过点(0,2)与双曲线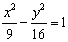 有且仅有一个公共点的直线的斜率的取值范围为______(答: 有且仅有一个公共点的直线的斜率的取值范围为______(答: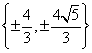 ); );
③过双曲线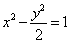 的右焦点作直线 的右焦点作直线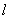 交双曲线于A、B两点,若 交双曲线于A、B两点,若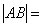 4,则满足条件的直线 4,则满足条件的直线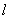 有____条(答:3); 有____条(答:3);
④对于抛物线C: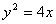 ,我们称满足 ,我们称满足 的点 的点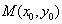 在抛物线的内部,若点 在抛物线的内部,若点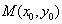 在抛物线的内部,则直线 在抛物线的内部,则直线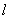 : :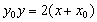 与抛物线C的位置关系是_______(答:相离); 与抛物线C的位置关系是_______(答:相离);
⑤过抛物线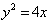 的焦点 的焦点 作一直线交抛物线于P、Q两点,若线段PF与FQ的长分别是 作一直线交抛物线于P、Q两点,若线段PF与FQ的长分别是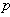 、 、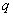 ,则 ,则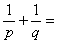 _______(答:1); _______(答:1);
⑥设双曲线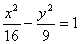 的右焦点为 的右焦点为 ,右准线为 ,右准线为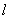 ,设某直线 ,设某直线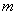 交其左支、右支和右准线分别于 交其左支、右支和右准线分别于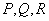 ,则 ,则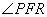 和 和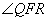 的大小关系为___________(填大于、小于或等于) (答:等于); 的大小关系为___________(填大于、小于或等于) (答:等于);
⑦求椭圆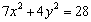 上的点到直线 上的点到直线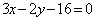 的最短距离(答: 的最短距离(答: ); );
⑧直线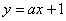 与双曲线 与双曲线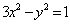 交于 交于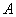 、 、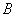 两点。①当 两点。①当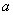 为何值时, 为何值时,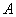 、 、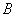 分别在双曲线的两支上?②当 分别在双曲线的两支上?②当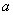 为何值时,以AB为直径的圆过坐标原点?(答:① 为何值时,以AB为直径的圆过坐标原点?(答:①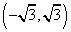 ;② ;②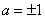 ); );
7、焦半径(圆锥曲线上的点P到焦点F的距离)的计算方法:利用圆锥曲线的第二定义,转化到相应准线的距离,即焦半径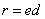 ,其中 ,其中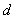 表示P到与F所对应的准线的距离。比如: 表示P到与F所对应的准线的距离。比如:
①已知椭圆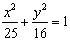 上一点P到椭圆左焦点的距离为3,则点P到右准线的距离为____(答: 上一点P到椭圆左焦点的距离为3,则点P到右准线的距离为____(答: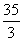 ); );
②已知抛物线方程为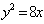 ,若抛物线上一点到 ,若抛物线上一点到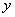 轴的距离等于5,则它到抛物线的焦点的距离等于____; 轴的距离等于5,则它到抛物线的焦点的距离等于____;
③若该抛物线上的点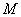 到焦点的距离是4,则点 到焦点的距离是4,则点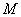 的坐标为_____(答: 的坐标为_____(答: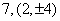 ); );
④点P在椭圆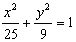 上,它到左焦点的距离是它到右焦点距离的两倍,则点P的横坐标为_______(答: 上,它到左焦点的距离是它到右焦点距离的两倍,则点P的横坐标为_______(答: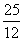 ); );
⑤抛物线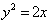 上的两点A、B到焦点的距离和是5,则线段AB的中点到 上的两点A、B到焦点的距离和是5,则线段AB的中点到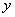 轴的距离为______(答:2); 轴的距离为______(答:2);
⑥椭圆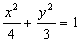 内有一点 内有一点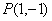 ,F为右焦点,在椭圆上有一点M,使 ,F为右焦点,在椭圆上有一点M,使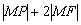 之值最小,则点M的坐标为_______(答: 之值最小,则点M的坐标为_______(答: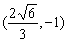 ); );
(责任编辑:admin) |
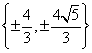 );
);