|
湖南省常德市安乡县第五中学 龚光勇收集整理 1、三个公理和三条推论： （1）公理1：一条直线的两点在一个平面内，那么这条直线上的所有的点都在这个平面内。这是判断直线在平面内的常用方法。 （2）公理2、如果两个平面有两个公共点，它们有无数个公共点，而且这无数个公共点都在同一条直线上。这是判断几点共线（证这几点是两个平面的公共点）和三条直线共点（证其中两条直线的交点在第三条直线上）的方法之一。 （3）公理3：经过不在同一直线上的三点有且只有一个平面。推论1：经过直线和直线外一点有且只有一个平面。推论2：经过两条相交直线有且只有一个平面。推论3：经过两条平行直线有且只有一个平面。公理3和三个推论是确定平面的依据。比如： ①在空间四点中，三点共线是四点共面的_____条件（答：充分非必要）； ②给出命题：①若A∈l，A∈α，B∈l ，B∈α，则 l  α；②若A∈α，A∈β，B∈α，B∈β，则α∩β＝AB；③若l α ，A∈l，则A α ④若A、B、C∈α，A、B、C∈β，且A、B、C不共线，则α与β重合。上述命题中，真命题是_____（答：①②④）；③长方体中ABCD-A1B1C1D1中，AB=8，BC=6，在线段BD，A1C1上各有一点P、Q，在PQ上有一点M，且PM=MQ，则M点的轨迹图形的面积为_______（答：24） 2、直观图的画法（斜二侧画法规则）：在画直观图时，要注意： （1）使  ， 所确定的平面表示水平平面。（2）已知图形中平行于  轴和 轴的线段，在直观图中保持长度和平行性不变，平行于 轴的线段平行性不变，但在直观图中其长度为原来的一半。比如：①用斜二测画法画一个水平放置的平面图形为如下图的一个正方形，则原来图形的形状是（ ）（答：A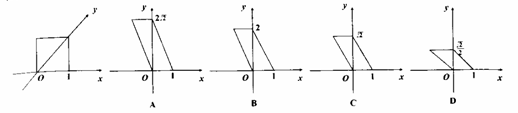）  ②已知正  的边长为 ，那么的平面直观图 的面积为_____（答： ）3、空间直线的位置关系：（1）相交直线――有且只有一个公共点。（2）平行直线――在同一平面内，没有公共点。（3）异面直线――不在同一平面内，也没有公共点。比如： ①空间四边形ABCD中，E、F、G、H分别是四边上的中点，则直线EG和FH的位置关系_____（答：相交）； ②给出下列四个命题：①异面直线是指空间既不平行又不相交的直线；②两异面直线  ，如果平行于平面 ，那么 不平行平面；③两异面直线，如果 平面，那么不垂直于平面；④两异面直线在同一平面内的射影不可能是两条平行直线。其中正确的命题是_____（答：①③）4、异面直线的判定：反证法。 比如： （1）“ａ、ｂ为异面直线”是指：①ａ∩ｂ＝Φ，但ａ不平行于ｂ；②ａ 面α，ｂ面β且a∩b＝Φ；③ａ面α，ｂ面β且α∩β＝Φ；④ａ面α，b面α ；⑤不存在平面α，能使ａ面α且ｂ面α成立。上述结论中，正确的是_____（答：①⑤）；（2）在空间四边形ABCD中，M、N分别是AB、CD的中点，设BC+AD=2a，则MN与a的大小关系是_____（答：MN<a）； （3）若E、F、G、H顺次为空间四边形ABCD四条边AB、BC、CD、DA的中点，且EG=3，FH=4，则AC2+BD2= _____（答：50）； （4）如果ａ、ｂ是异面直线，P是不在ａ、ｂ上的任意一点，下列四个结论：①过点P一定可以作直线  与ａ、ｂ都相交； ②过点P一定可以作直线与ａ、ｂ都垂直；③过点P一定可以作平面α与ａ、ｂ都平行； ④过点P一定可以作直线与ａ、ｂ都平行。其中正确的结论是_____（答：②）；（5）如果两条异面直线称作一对，那么正方体的十二条棱中异面直线的对数为_____（答：24）； （6）已知平面  求证：b、c是异面直线．5、异面直线所成角  的求法：（1）范围： ；（2）求法：计算异面直线所成角的关键是平移（中点平移，顶点平移以及补形法：把空间图形补成熟悉的或完整的几何体，如正方体、平行六面体、长方体等，以便易于发现两条异面直线间的关系）转化为相交两直线的夹角。比如：（1）正四棱锥  的所有棱长相等， 是 的中点，那么异面直线 与 所成的角的余弦值等于____（答： ）；（2）在正方体AC1中，M是侧棱DD1的中点，O是底面ABCD的中心，P是棱A1B1上的一点，则OP与AM所成的角的大小为____（答：90°）； （3）已知异面直线a、b所成的角为50°，P为空间一点，则过P且与a、b所成的角都是30°的直线有且仅有____条（答：2）； （4）若异面直线 所成的角为 ，且直线 ，则异面直线 所成角的范围是____（答： ）；6、异面直线的距离的概念：和两条异面直线都垂直相交的直线叫异面直线的公垂线。两条异面直线的公垂线有且只有一条。而和两条异面直线都垂直的直线有无数条，因为空间中，垂直不一定相交。比如： （1）ABCD是矩形，沿对角线AC把ΔADC折起，使AD⊥BC，求证：BD是异面直线AD与BC的公垂线； （2）如图，在正方体ABCD—A1B1C1D1中，EF是异面直线AC与A1D的公垂线，则由正方体的八个顶点所连接的直线中，与EF平行的直线有____条（答：1）；  7、两直线平行的判定： （1）公理4：平行于同一直线的两直线互相平行； （2）线面平行的性质：如果一条直线和一个平面平行，那么经过这条直线的平面和这个平面相交的交线和这条直线平行； （3）面面平行的性质：如果两个平行平面同时与第三个平面相交，那么它们的交线平行； （4）线面垂直的性质：如果两条直线都垂直于同一个平面，那么这两条直线平行。 8、两直线垂直的判定：（1）转化为证线面垂直；（2）三垂线定理及逆定理。 9、直线与平面的位置关系：（1）直线在平面内；（2）直线与平面相交。其中，如果一条直线和平面内任何一条直线都垂直，那么这条直线和这个平面垂直。 注意：任一条直线并不等同于无数条直线；（3）直线与平面平行。其中直线与平面相交、直线与平面平行都叫作直线在平面外。比如： （1）下列命题中，正确的是 A、若直线 平行于平面内的一条直线b , 则 // B、若直线 垂直于平面的斜线b在平面内的射影，则⊥b C、若直线 垂直于平面,直线b是平面的斜线，则与b是异面直线 D、若一个棱锥的所有侧棱与底面所成的角都相等，且所有侧面与底面所成的角也相等，则它一定是正棱锥（答：D）； （2）正方体ABCD-A1B1C1D1中，点P在侧面BCC1B1及其边界上运动，并且总保持AP⊥BD1，则动点P的轨迹是___________（答：线段B1C）。 10、直线与平面平行的判定和性质： （1）判定：①判定定理：如果平面内一条直线和这个平面平面平行，那么这条直线和这个平面平行；②面面平行的性质：若两个平面平行，则其中一个平面内的任何直线与另一个平面平行。 （2）性质：如果一条直线和一个平面平行，那么经过这条直线的平面和这个平面相交的交线和这条直线平行。在遇到线面平行时，常需作出过已知直线且与已知平面相交的辅助平面，以便运用线面平行的性质。比如： （1）α、β表示平面，a、b表示直线，则a∥α的一个充分不必要条件是 A、α⊥β，a⊥β B、α∩β＝b，且a∥b C、a∥b且b∥α D、α∥β且a β（答：D）；（2）正方体ABCD-A１B１C１D１中，点N在BD上，点M在B1C上，且CM=DN，求证：MN∥面AA1B1B。 11、直线和平面垂直的判定和性质： （1）判定：①如果一条直线和一个平面内的两条相交直线都垂直，那么这条直线和这个平面垂直。②两条平行线中有一条直线和一个平面垂直，那么另一条直线也和这个平面垂直。 （2）性质：①如果一条直线和一个平面垂直，那么这条直线和这个平面内所有直线都垂直。②如果两条直线都垂直于同一个平面，那么这两条直线平行。比如： （1）如果命题“若  ∥z，则 ”不成立，那么字母x、y、z在空间所表示的几何图形一定是_____（答：x、y是直线，z是平面）；（2）已知a，b，c是直线，α、β是平面，下列条件中能得出直线a⊥平面α的是 A、a⊥b，ａ⊥ｃ其中ｂ α，ｃα B、a⊥b ，ｂ∥α C、α⊥β，ａ∥β D、ａ∥ｂ，ｂ⊥α（答：D）； （3）AB为⊙O的直径，C为⊙O上的一点，AD⊥面ABC，AE⊥BD于E，AF⊥CD于F，求证：BD⊥平面AEF。 12、三垂线定理及逆定理： （1）定理：在平面内的一条直线，如果它和这个平面的一条斜线的射影垂直，那么它也和这条斜线垂直。 （2）逆定理：在平面内的一条直线，如果它和这个平面的一条斜线，那么它也和这条斜线在平面内的射影垂直。其作用是证两直线异面垂直和作二面角的平面角。 13、直线和平面所成的角： （1）定义：平面的一条斜线和它在平面内的射影所成的锐角，叫这条直线和这个平面所成的角。 （2）范围：  ；（3）求法：作出直线在平面上的射影；（4）斜线与平面所成的角的特征：斜线与平面中所有直线所成角中最小的角。比如： （1）在正三棱柱ABC-A1B1C1中，已知AB=1，D在棱BB1上，BD=1，则AD与平面AA1C1C所成的角为______（答：arcsin  ）；（2）正方体ABCD-A1B1C1D1中，E、F分别是AB、C1D1的中点，则棱 A1B1 与截面A1ECF所成的角的余弦值是______（答：  ）；（3）  是从点 引出的三条射线，每两条的夹角都是 ，则直线与平面 所成角的余弦值为______（答：）；（4）若一平面与正方体的十二条棱所在直线都成相等的角θ，则sinθ的值为______（答： ）。14、平面与平面的位置关系：（1）平行――没有公共点；（2）相交――有一条公共直线。 15、两个平面平行的判定和性质： （1）判定：一个如果平面内有两条相交直线和另一个平面平行，则这两个平面平行。 （2）性质：如果两个平行平面同时与第三个平面相交，那么它们的交线平行。比如： （1）  是两个不重合的平面，在下列条件中，不能判定平面 的条件是A、  是内一个三角形的两条边，且 B、 内有不共线的三点到 的距离都相等 C、 都垂直于同一条直线 D、 是两条异面直线， ，且 （答：B）；（2）给出以下六个命题：①垂直于同一直线的两个平面平行；②平行于同一直线的两个平面平行；③平行于同一平面的两个平面平行；④与同一直线成等角的两个平面平行；⑤一个平面内的两条相交直线于另一个平面内的两条相交直线平行，则这两个平面平行；⑥两个平面分别与第三个平面相交所得的两条交线平行，则这两个平面平行。其中正确的序号是___________（答：①③⑤）； （3）正方体ABCD-A１B１C１D１中AB= 。①求证：平面AD1B1∥平面C1DB；②求证：A1C⊥平面AD1B1 ；③求平面AD1B1与平面C1DB间的距离（答： ）；16、二面角： （1）平面角的三要素：①顶点在棱上；②角的两边分别在两个半平面内；③角的两边与棱都垂直。 （2）作平面角的主要方法：①定义法：直接在二面角的棱上取一点（特殊点），分别在两个半平面内作棱的垂线，得出平面角，用定义法时，要认真观察图形的特性；②三垂线法：过其中一个面内一点作另一个面的垂线，用三垂线定理或逆定理作出二面角的平面角；③垂面法：过一点作棱的垂面，则垂面与两个半平面的交线所成的角即为平面角； （3）二面角的范围：  ；（4）二面角的求法：①转化为求平面角；②面积射影法：利用面积射影公式  ，其中为平面角的大小。对于一类没有给出棱的二面角，应先延伸两个半平面，使之相交出现棱，然后再选用上述方法（尤其可考虑面积射影法）。比如：（1）正方形ABCD-A1B1C1D1中，二面角B-A1C-A的大小为________（答：  ）；（2）将∠A为60°的棱形ABCD沿对角线BD折叠，使A、C的距离等于BD，则二面角A-BD-C的余弦值是______（答： ）；（3）正四棱柱ABCD—A1B1C1D1中对角线BD1＝8，BD1与侧面B1BCC1所成的为30°，则二面角C1—BD1—B1的大小为______（答：  ）；（4）从点P出发引三条射线PA、PB、PC，每两条的夹角都是60°，则二面角B-PA-C的余弦值是______（答： ）；（5）二面角α-  -β的平面角为120°，A、B∈，ACα，BDβ，AC⊥，BD⊥，若AB=AC=BD=1，则CD的长______（答：2）；（6）ABCD为菱形，∠DAB＝60°，PD⊥面ABCD，且PD＝AD，则面PAB与面PCD所成的锐二面角的大小为______（答：  ）。17、两个平面垂直的判定和性质： （1）判定：①判定定理：如果一个平面经过另一个平面的一条垂线，那么这两个平面互相垂直。②定义法：即证两个相交平面所成的二面角为直二面角； （2）性质：如果两个平面垂直，那么在一个平面内垂直于它们交线的直线垂直于另一个平面。比如： （1）三个平面两两垂直，它们的交线交于一点O，P到三个面的距离分别为3、4、5，则OP的长为_____（答：5）； （2）在四棱锥P-ABCD中，PA⊥底面ABCD，底面各边都相等，M是PC上的一动点，当点M满足___________时，平面MBD⊥平面PCD（答：  ）；（3）过S引三条长度相等但不共面的线段SA、SB、SC，且∠ASB=∠ASC=60°，∠BSC＝90°，求证：平面ABC⊥平面BSC。 特别指出：立体几何中平行、垂直关系的证明的基本思路是利用线面关系的转化，即：  如（1）已知直线  平面，直线 平面，给出下列四个命题：① ；② ；③ ；④ 。其中正确的命题是_____（答：①③）；（2）设是两条不同直线，是两个不同平面，给出下列四个命题：①若 则 ；②若 ，则 ；③若 ，则 或 ；④若 则 。其中正确的命题是_____（答：①③④）18、空间距离的求法：（特别强调：立体几何中有关角和距离的计算，要遵循“一作，二证，三计算”的原则） （1）异面直线的距离：①直接找公垂线段而求之；②转化为求直线到平面的距离，即过其中一条直线作平面和另一条直线平行。③转化为求平面到平面的距离，即过两直线分别作相互平行的两个平面。 如已知正方体ABCD- A1B1C1D1的棱长为 ，则异面直线BD与B1C的距离为_____（答：）。（2）点到直线的距离：一般用三垂线定理作出垂线再求解。比如： ①等边三角形  的边长为 ， 是 边上的高，将 沿折起，使之与 所在平面成 的二面角，这时 点到的距离是_____（答： ）；②点P是120°的二面角α- -β内的一点，点P到α、β的距离分别是3、4，则P到的距离为 _______（答： ）；③在正方体ABCD—A1B1C1D1的侧面AB1内有一动点P到棱A1B1与棱BC的距离相等，则动点P所在曲线的形状为_______（答：抛物线弧）。 （3）点到平面的距离：①垂面法：借助于面面垂直的性质来作垂线，其中过已知点确定已知面的垂面是关键；②体积法：转化为求三棱锥的高；③等价转移法。比如： ①长方体  的棱 ，则点 到平面 的距离等于______（答： ）；②在棱长为a的正方体ABCD-A1B1C1D1中，M是AA1的中点，则A1到平面MBD的距离为______（答：  a）。（4）直线与平面的距离：前提是直线与平面平行，利用直线上任意一点到平面的距离都相等，转化为求点到平面的距离。 （5）两平行平面之间的距离：转化为求点到平面的距离。 （6）球面距离（球面上经过两点的大圆在这两点间的一段劣弧的长度）：求球面上两点A、B间的距离的步骤：①计算线段AB的长；②计算球心角∠AOB的弧度数；③用弧长公式计算劣弧AB的长。比如： ①设地球半径为  ，在北纬 圈上有 两地，它们的纬度圈上的弧长等于 ，求两地间的球面距离（答： ）；②球面上有3点，其中任意两点的球面距离都等于大圆周长的  ，经过这3点的小圆的周长为 ，那么这个球的半径为______（答： ）；③三棱锥  的三个侧面两两垂直， ，若 四个点都在同一球面上，则此球面上两点A、B之间的球面距离是_________（答： ）。(责任编辑：admin) |