|
广东省中山市东升高中 高建彪 如果每个事件发生的概率只与构成该事件区域的长（面积或体积）成比例，则称这样的概率模型为几何概率模型（geometric models of probability），简称为几何概型. 在几何概型中，事件A的概率计算公式为：  .用几何概率公式计算概率时，关键是构造出随机事件所对应的几何图形，并对几何图形进行相应的几何度量. 对于一些简单的几何概型问题，可以快捷的找到解决办法. 例1 如图，以正方形ABCD的边长为直径作半圆，重叠部分为花瓣. 现在向该矩形区域内随机地投掷一飞镖，求飞镖落在花瓣内的概率. 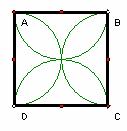 解：飞镖落在正方形区域内的机会是均等的，符合几何概型条件. 记飞镖落在花瓣内为事件A，设正方形边长为2r，则  .所以，飞镖落在花瓣内的概率为  .点评：此题的关键是正确计算花瓣的面积. 这类题型中，试验全部结果的区域与构成事件A的区域，都直接由题中条件给出，从而易解. 然而，有些几何概型的问题，既不容易分辩出属于几何概率模型，也难发现随机事件的构成区域，但仔细研究此类问题后，我们可以发现一些解题的规律. 例2 两人相约7点到8点在某地会面，先到者等候另一人20分钟，过时离去. 求两人能够会面的概率. 解：设两人到达的时间分别为7点到8点之间的x分钟、y分钟.用  表示每次试验的结果，则所有可能结果为： ；记两人能够会面为事件A，则事件A的可能结果为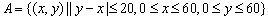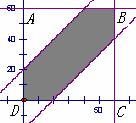：  . 如图所示，试验全部结果构成区域Ω为正方形ABCD. 而事件A所构成区域是正方形内两条直线  ， 所夹中间的阴影部分. 根据几何概型公式，得到： .所以，两人能够会面的概率为  .点评：题目的意思简单明了，但如何转化为数学模型来求解却比较困难. 需要我们先从实际问题中分析得到存在的两个变量，如此题中两人到达的时间都是随机的，设为两个变量. 然后把这两个变量所满足的条件写成集合形式，并把所研究事件A的集合也分析得出. 把两个集合用平面区域表示，特别注意不等式所表示区域. 我们可以发现，要表示二元一次不等式  的平面区域，按两步解决：（1）作出直线；（2）取一特殊点验证，直线的哪侧符合不等式，则哪侧就是所表示区域. 准确得到随机事件的构成区域后，根据几何概型的概率公式，易求得概率.根据以上的解法和分析，我们把此类疑难问题的解决总结为以下四步： （1）构设变量. 从问题情景中，发现哪两个量是随机的，从而构设为变量x、y. （2）集合表示. 用 表示每次试验结果，则可用相应的集合分别表示出试验全部结果Ω和事件A所包含试验结果. 一般来说，两个集合都是几个二元一次不等式的交集.（3）作出区域. 把以上集合所表示的平面区域作出，先作不等式对应的直线，然后取一特殊点验证哪侧是符合条件的区域. （4）计算求解. 根据几何概型的公式，易从平面图形中两个面积的比求得. 在以上四步曲中，第二步和第三步是解答的关键，通过这两步，可以发现随机事件所对应的几何图形. 第三步的作图需理解其原理. 下面依据这四步曲再解一题. 例3 一条直线型街道的A、B两盏路灯之间的距离为120米，由于光线较暗，想在中间再随意安装两盏路灯C、D，顺序为A、C、D、B. 问A与C、B与D之间的距离都不小于40米的概率是多少？ 解：（1）构设变量. 设A与C、B与D之间的距离分别为x米、y米. （2）集合表示. 用 表示每次试验的结果，则所有可能结果为：  ；记A与C、B与D之间的距离都不小于40米为事件A，则事件A的可能结果为 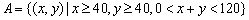 .（3）作出区域. 如图所示，试验全部结果构成区域Ω为直线 与两坐标轴所围成的△ABC. 而事件A所构成区域是三条直线 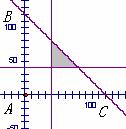 ， ， 所夹中间的阴影部分. （4）计算求解. 根据几何概型公式，得到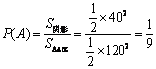：  .所以，A与C、B与D之间的距离都不小于40米的概率为  .点评：此题易错误的认为，把AB三等分，由于中间长度为40米，所以路灯C与D需安装在中间一段，从而CD安装在中间的概率为  . 错误的原因是试验的结果不可能独立地安装在这三段，有可能跨这三段中的两段安装. 用以上四步曲求解，我们可以得到清晰的解题思路. (责任编辑：admin) |