|
1.根据国家版权局《书籍稿酬暂行规定》,书籍稿酬由基本稿酬和印数稿酬组成。 基本稿酬的标准为:(1)著作稿酬每千字10至30元,确有学术价值的,可适当提高,但每千字不超过40元;(2)词书稿有两种计酬方法:其一是按一般著作稿标准另加15%至20%计算(词条书目);其二是按每千字20元至30元计算,另增加20%至30%的基本稿酬(百科全书词条)。 印数稿酬的标准为:(1)一般书籍,印数在一万册以内的,以一万册计算付基本稿酬的8%。印数超过一万册的,其超过部分每千册付基本稿酬的0.8%。(2)确有学术价值而印数较少的专著,印数在一万册以内的,以一万册计算付基本稿酬的30%,印数超过一万册的,计算方法同(1)。 根据以上内容,解答下列问题。 (1) 若印x 千册,试写出每千字最高稿酬f(x) 和每千字最低稿酬g(x) 的函数关系式; (2) 若王教授出版了一本25.4万字的书,印数1.8万册,试计算他可获得的最高稿酬和最低稿酬。 2.小童的父亲要到美国访问,受人之托希望多带点东西。中国民航的《国际旅客须知》中有关规定:"计件免费行李额"中规定"适用中美、中加国际航线上的行李运输……。经济和旅游折扣票价,免费交运的行李数为两件,每件箱体三边之和不超过62英寸(158厘米),但两件之和不得超过107英寸(273厘米),每件最大重量不得超过32公斤。"试问这两个箱子的长、宽、高各为多少可达最大体积? 请到市场上看看,商店出售的行李箱的尺寸与你计算所得结果是否近似?为什么? 3. 今年年初由中国建设银行北京市分行印发的《个人住房贷款简介》的小 册子中介绍了有关个人住房贷款的有关问题。其中指明贷款额最高为拟购买住房费用总额的70%;贷款期限最长为20年。个人住房贷款利率如附表1所示。借款人在借款期内每月以相等的月均还款额偿还银行贷款本金和利息。附表2列出了不同贷款期限下的月均还款额、还款总额和利息负担总和。试给出公式说明附表2中后三列数是如何算出来的。 近年来国务院批准,中国人民银行决定从1999年9月21日起,延长个人住房贷款期限并降低利率以支持城镇居民购房。各商业银行个人住房贷款的最长期限由现行的20年延长到30年。每笔贷款年限由商业银行依据借款个人的年龄、工作年限、还款能力等因素与借款人协商确定。个人住房款年利率最高水平降为5.88%。并根据贷款期限划分为两个档次:5年以下(含5年)为年利率5.31,5年以上为年利率5.88%。 请你根据新规定计算5年期、20年期的月均还款额、还款总额和利息负担总和,并与原附表2中的同期贷款的负担情况比较,住房贷款的负担各降低了多少。
附表2 中国建设银行北京分行个人住房贷款1~20年月均还款金额表 (借款额为壹万元) 单位:元
(本表自1998年12月7日起执行) 4. 某化工厂从今年一月起,若不改善生产环境,按现状生产,每月收入为70万元,同时将受到环保部门的处罚,第一个月罚3万元,以后逐月递增2万元。如果从今年一月起投资500万元增加回收净化设备(改造设备时间不计),一方面可以改善环境,另一方面也可以大大降低原料成本。据测算投产后的前5个月中的累计净收入是生产时间 n(以月为单位)的二次函数,生产前1、前2、前3个月的累计收入分别可达101万元、204万元和309万元,以后稳定在第5个月的水平。同时该厂不但不受罚,而且还将得到环保部门一次性100万元的奖励。问经过多少个月,投资开始见效,即投资改造后的纯收入多于不改造时的纯收入。 5. 据世界人口组织公布,地球上的人口在公元元年为2.5亿,1600年为5亿,1830年为10亿,1930年为20亿,1960年为30亿,1974年为40亿,1987年为50亿,到1999年底,地球上的人口数达到了60亿。请你根据20世纪人口增长规律推测,到哪年世界人口将达到100亿?到2100年地球上将会有多少人口? 6. 国庆庆典活动的中心广场有数万名学生手持圆花组成大型图案方阵,方阵前排距观礼台120米,方阵纵列95人,每列长度192米,问第一、二排间距多大能达到满意的观礼效果? 7. 在某1000个人中有10个人患有一种病,现要通过验血把这10个病人 查出来,若采用逐个人化验的方法需化验999次,(这里所需化验次数是指在最坏情况下化验次数,如果碰巧,可能首先化验的10个人全是病人,10次化验就够了。下面讨论的化验次数均指最坏情况下的化验次数)。 为了减少化验次数,人们采用分组化验的办法,即把几个人的血样混在一起,先化验一次,若化验合格,则这几个人全部正常,若混合血样不合格,说明这几个人中有病人,再对它们重新化验(逐个化验,或再分成小组化验)。 试给出一种分组化验方法使其化验次数尽可能地小,不超过100次。 参考解答 1.解 (1) 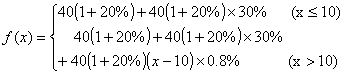 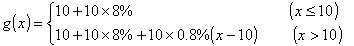 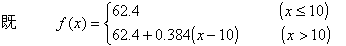 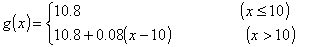 (2)此时x=18,f(18)=65.472,g(18)=11.44 ,因此此书25.4万字(254千字),所以最高稿酬为 65.472×254=16629.888≈16629.89(元),最低稿酬为11.44×254=2095.76 (元) 2.解 设长、宽、高分别为a,b,c 显然a>0,b>0,c>0. 若a+b+c 一定(≤158), 根据a+b+c≥ 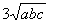 ,当且仅当a=b=c 时等号成立,因此箱子为正方体时体积最大。 ,当且仅当a=b=c 时等号成立,因此箱子为正方体时体积最大。 设两个正方体箱子的边长分别为a,b,(a>0,b>0). 由条件知 3(a+b)≤273,,为求最大取等号,故得 a+b=91 设 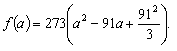 显然,当 显然,当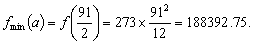 根据题意及上述,要在 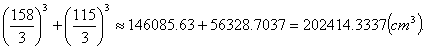 市场调查思考: ① 商店出售的箱子三边长与计算所得误差很大,原因: (1) 正方体箱子不易携带。 (2) 正方体箱子容量大,但易超重。 ② 很多货运箱的形状与手提行李箱相比,近似于正方体,因为货运箱可更多地考虑其容积问题。 3.解 设贷款额(本金)为A(元),货款期限为n(月),月利率为  ,月均还款额为B,令 ,月均还款额为B,令  为第k 个月末还款后的本利金额,则 为第k 个月末还款后的本利金额,则   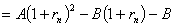 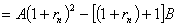 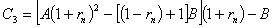 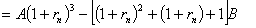 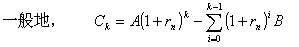 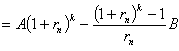 根据题意,当k=n 时, 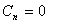 ,于是 ,于是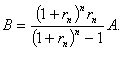 例如贷款期5年时, 由 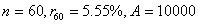 元,得 元,得 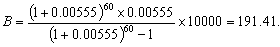 还款总额 60B=11784.60,利息负担总额60B-A=1784.60 ,得到附表2上相应的值。 降低货款利率后, 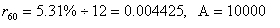 月均还款 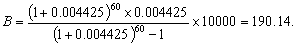 总还款 60B=11408.4,总利息60B-A=1408.4 ,与原附表2中的同期货款的负提相比,每月少交6.27 元。一共少负担376.2 元。 对于n>60(10年), 4.解 设不改造设备,按原条件生产,n 个月累计收入为a(n),改造设备后生产,n个月累计收入为b(n)。由已知条件a(n)=70n,且可设 101=b(1)=a+b+c 204=b(2)=4a+2b+c 309=b(3)=9a+3b+c 解此方程组,得到a=1, b=100, c=0 于是 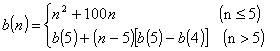 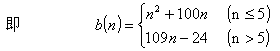 经过简单计算可以发现,5个月内投资不能见效。这是因为 b(5)-500+100=125<315=a(5)-[3+5+7+9+11], 令 b(n)-500+100>a(n)-[3n+2n(n-1))/2] , (n>5), 即 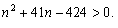 当 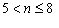 时 时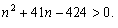 当 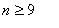 时 时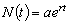 所以,经过9个月投资才可见效。 5.解 题目中的数据均为大致时间,粗略估计的量,带有较多的误差。因此寻找人口增长规律时不需要,也不应该过分强调规律与数据完全吻合。数据中20世纪以前的人口资料更加粗略,况且人口的预报准确程度主要受到20世纪人口增长规律的影响,因而组建预报模型时,不必要考虑20世纪以前的数据资料,在20世纪人口增长速度是逐渐变快的,因此用直线变化(匀速增长)建模做预报是不恰当的;做为人口增长的模型,一般可以使用指数关系 将 模型为 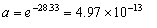 (亿) (1930≤t≤1999) (亿) (1930≤t≤1999)模型的拟合效果为 (人口单位:亿) 年 代 1930 1960 1974 1987 1999 人口数 20 30 40 50 60 拟合数 19.49 31.70 39.78 49.11 56.61 拟合效果较好,可用于预报。 令N(t)=100 ,可求出t=2030.84 ,故可知如果照此规律大约在2031年世界人口将达到100亿,而于2100年世界人口将达到307亿。 6.解 下面给出一个简单的解法,但它是较粗糙的,不过也实用。 所谓满意,可以认为从观礼位置看到的纵列上每个花的部分是一样的。  设观礼者居高a 米,从观礼位置看到的纵列上每个花的部分高度为b 米。 依题意,每列从第一个人到最后一个人(第95人)有94个间空,列长192米,则每列相邻二人平均间距约2米。 为简单起见,不妨设位于192米长的队列中点前后的两人间隔是2米,则  设第一、二排间距为 x米,则  于是,  (米) (米) 7.解 我们给出如下的方法: 从1000人中任取64人,把他们的血样混合化验(一般地,n 个人中有k 个病人,令s 使 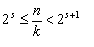 ,则从n 个人中任取 ,则从n 个人中任取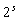 个人一组,当n=1000 ,k=10 时, 个人一组,当n=1000 ,k=10 时,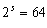 若这64人混合血样合格(化验是阴性),则这64个人正常,可排除,无需再化验,再从剩下未化验的人中任取64个人,混合血样化验。 若这64人混合血样不合格(化验呈阳性),说明这64人中有病人。把这64个人,分为两组,每组32人。 任取一组的混合血化验,即可确定有病人的一组。(即只需化验一次,若化验的这组血样成阴性,则病人在另一组。若化验的这组血样成阳性,这组有病人,但此时,另一组也可能有病人)。作为最坏的可能情形,我们无法保证另一组的32人中没有病人,故选定有病人的一组后,把另一组人退回到未化验的人群中去。 把有病人的这组32人,再分为两组,每组16人,重复上述过程。即化验一次,确定有病人的一组,把另一组退回到未化验的人群中。 依次下去,直到找到一个病人为止。至此一共化验了7次。 再从未化验的人中任取64人重复上述过程。 总之,对每次64人混合血化验成阳性的,通过7次化验可找到1个病人,由于共有10个病人,因此,这样的情形,化验次数不超过7×10=70 次。对每次64人混合血化验成阴性的,由于1000=15×64+40 ,化验次数不超过15次。 故总的化验次数不超过70+15=85次。 (责任编辑:admin) |
