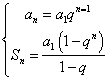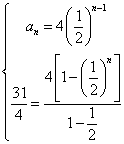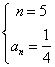|
(一)等差数列公式 1.等差数列公式： 通项公式an=a1+(n-1)d （首项a1,公差d, an第n项数） ak=ak+(n-k)d ak为第k项数 若a,A,b构成等差数列 则 A=(a+b)/2 2.等差数列前n项和公式: 设等差数列的前n项和为Sn 即 Sn=a1+a2+...+an; 那么 Sn=na1+n(n-1)d/2=dn2/2+(a1-d/2)n (二)等比数列公式 1.等比数列公式: 通项公式 an=a1q(n-1)(a1为首项，an为第n项) an=a1q(n-1),am=a1q(m-1) 则an/am=q(n-m) (1)an=amq(n-m) (2)a,G,b 若构成等比中项，则G2=ab (a,b,G≠0) (3)若m+n=p+q，则 aman=apaq 2.等比数列前n项和公式 设 a1,a2,a3...an构成等比数列 前n项和Sn=a1+a2+a3...an Sn=a1+a1q+a1q2+....a1q(n-2)+a1q(n-1) Sn=a1(1-qn)/(1-q)=(a1-anq)/(1-q); 注： q≠1; Sn=na1 注:q=1 （三）例题精讲： 例1．运用公式解决国王赏麦故事中的难题。
变式练习：⑴求等比数列1,2,4,8…的前多少项和是63.
⑵求等比数列1,2,4,8…第4项到第7项的和.
例2．画一个边长为2cm的正方形，再将这个正方形各边的中点相连得到第2个正方形，
依次类推⑴若一共画了7个正方形，求第7个正方形的面积？
⑵若已知所画正方形的面积和为
解：由题意得：每个正方形的面积构成等比数列，且
（1）
（2）
答：（1）第七个正方形的面积是
（2）一共测了5个正方形，所画的最后一个正方形的面积是
巩固练习：⑴已知等比数列
⑵已知等比数列 |
，求一共画了几个正方形，及所画的最后一个正方形的面积。
。
。
中，
，
,求
。 
，
,
，求n，
。