34、(全国一文 20)设函数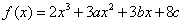 在 在 及 及 时取得极值. 时取得极值.
(Ⅰ)求a、b的值;
(Ⅱ)若对于任意的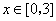 ,都有 ,都有 成立,求c的取值范围. 成立,求c的取值范围.
【解答】(Ⅰ)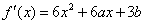 , ,
因为函数 在 在 及 及 取得极值,则有 取得极值,则有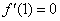 , , . .
即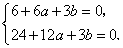
解得 , ,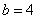 . .
(Ⅱ)由(Ⅰ)可知, , ,
 . .
当 时, 时,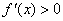 ; ;
当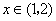 时, 时, ; ;
当 时, 时,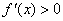 . .
所以,当 时, 时, 取得极大值 取得极大值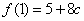 ,又 ,又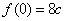 , ,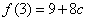 . .
则当 时, 时, 的最大值为 的最大值为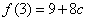 . .
因为对于任意的 ,有 ,有 恒成立, 恒成立,
所以  , ,
解得  或 或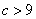 , ,
因此 的取值范围为 的取值范围为 . .
35、(全国二理 22)已知函数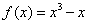 . .
(1)求曲线 在点 在点 处的切线方程; 处的切线方程;
(2)设 ,如果过点 ,如果过点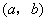 可作曲线 可作曲线 的三条切线,证明: 的三条切线,证明: . .
【解答】(1)求函数 的导数; 的导数;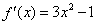 . .
曲线 在点 在点 处的切线方程为: 处的切线方程为:
 , ,
即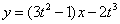 . .
(2)如果有一条切线过点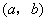 ,则存在 ,则存在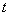 ,使 ,使
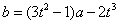 . .
于是,若过点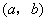 可作曲线 可作曲线 的三条切线,则方程 的三条切线,则方程

有三个相异的实数根.
记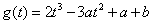 , ,
则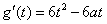
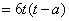 . .
当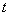 变化时, 变化时,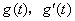 变化情况如下表: 变化情况如下表:
由 的单调性,当极大值 的单调性,当极大值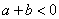 或极小值 或极小值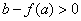 时,方程 时,方程 最多有一个实数根; 最多有一个实数根;
当 时,解方程 时,解方程 得 得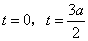 ,即方程 ,即方程 只有两个相异的实数根; 只有两个相异的实数根;
当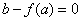 时,解方程 时,解方程 得 得 ,即方程 ,即方程 只有两个相异的实数根. 只有两个相异的实数根.
综上,如果过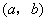 可作曲线 可作曲线 三条切线,即 三条切线,即 有三个相异的实数根,则 有三个相异的实数根,则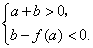
即  . .
36、(全国二文 22)已知函数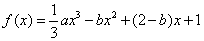 在 在 处取得极大值,在 处取得极大值,在 处取得极小值,且 处取得极小值,且 . .
(1)证明 ; ;
(2)若z=a+2b,求z的取值范围。
【解答】求函数 的导数 的导数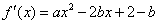 . .
(Ⅰ)由函数 在 在 处取得极大值,在 处取得极大值,在 处取得极小值,知 处取得极小值,知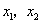 是 是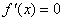 的两个根. 的两个根.
所以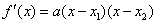
当 时, 时, 为增函数, 为增函数,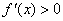 ,由 ,由 , , 得 得 . .
(Ⅱ)在题设下, 等价于 等价于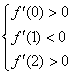 即 即 . .
化简得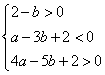 . .
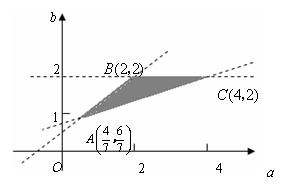
此不等式组表示的区域为平面 上三条直线: 上三条直线: . .
所围成的 的内部,其三个顶点分别为: 的内部,其三个顶点分别为: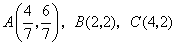 . .
 在这三点的值依次为 在这三点的值依次为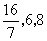 . .
所以 的取值范围为 的取值范围为 . .
37、(山东理 22)设函数 ,其中 ,其中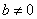 . .
(Ⅰ)当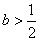 时,判断函数 时,判断函数 在定义域上的单调性; 在定义域上的单调性;
(Ⅱ)求函数 的极值点; 的极值点;
(Ⅲ)证明对任意的正整数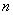 ,不等式 ,不等式 都成立. 都成立.
【解答】(Ⅰ)由题意知, 的定义域为 的定义域为 , ,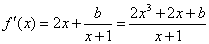
设 ,其图象的对称轴为 ,其图象的对称轴为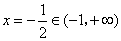 , ,
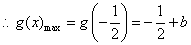 . .
当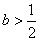 时, 时, , ,
即 在 在 上恒成立, 上恒成立,
 当 当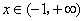 时, 时,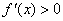 , ,
 当 当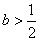 时,函数 时,函数 在定义域 在定义域 上单调递增. 上单调递增.
(Ⅱ)①由(Ⅰ)得,当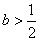 时,函数 时,函数 无极值点. 无极值点.
② 时, 时,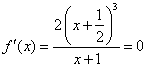 有两个相同的解 有两个相同的解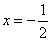 , ,
 时, 时,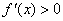 , ,
 时, 时,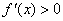 , ,
 时,函数 时,函数 在 在 上无极值点. 上无极值点.
③当 时, 时,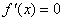 有两个不同解, 有两个不同解,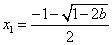 , ,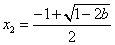 , ,
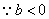 时, 时,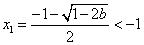 , ,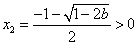 , ,
即 , , . .
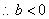 时, 时,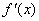 , , 随 随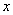 的变化情况如下表: 的变化情况如下表:
由此表可知: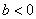 时, 时, 有惟一极小值点 有惟一极小值点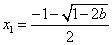 , ,
当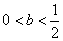 时, 时,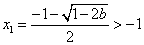 , ,
 , ,
此时,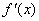 , , 随 随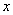 的变化情况如下表: 的变化情况如下表:
由此表可知: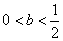 时, 时, 有一个极大值 有一个极大值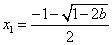 和一个极小值点 和一个极小值点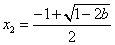 ; ;
综上所述:
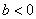 时, 时, 有惟一最小值点 有惟一最小值点 ; ;
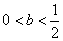 时, 时, 有一个极大值点 有一个极大值点 和一个极小值点 和一个极小值点 ; ;
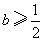 时, 时, 无极值点. 无极值点.
(Ⅲ)当 时,函数 时,函数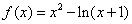 , ,
令函数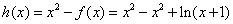 , ,
则 . .
 当 当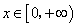 时, 时,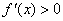 ,所以函数 ,所以函数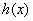 在 在 上单调递增, 上单调递增,
又 . .
 时,恒有 时,恒有 ,即 ,即 恒成立. 恒成立.
故当 时,有 时,有 . .
对任意正整数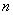 取 取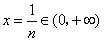 ,则有 ,则有 . .
所以结论成立.
38、(山东文 21)设函数 ,其中 ,其中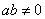 . .
证明:当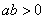 时,函数 时,函数 没有极值点;当 没有极值点;当 时,函数 时,函数 有且只有一个极值点,并求出极值. 有且只有一个极值点,并求出极值.
【解答】因为 ,所以 ,所以 的定义域为 的定义域为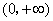 . .
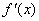 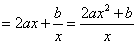 . .
当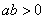 时,如果 时,如果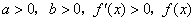 在 在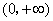 上单调递增; 上单调递增;
如果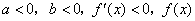 在 在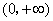 上单调递减. 上单调递减.
所以当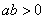 ,函数 ,函数 没有极值点. 没有极值点.
当 时, 时,

令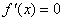 , ,
将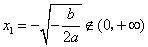 (舍去), (舍去), , ,
当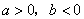 时, 时,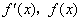 随 随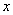 的变化情况如下表: 的变化情况如下表:
从上表可看出,
函数 有且只有一个极小值点,极小值为 有且只有一个极小值点,极小值为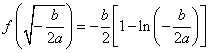 . .
当 时, 时,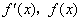 随 随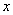 的变化情况如下表: 的变化情况如下表:
从上表可看出,
函数 有且只有一个极大值点,极大值为 有且只有一个极大值点,极大值为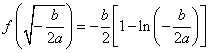 .综上所述, .综上所述,
当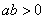 时,函数 时,函数 没有极值点; 没有极值点;
当 时, 时,
若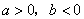 时,函数 时,函数 有且只有一个极小值点,极小值为 有且只有一个极小值点,极小值为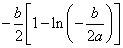 . .
若 时,函数 时,函数 有且只有一个极大值点,极大值为 有且只有一个极大值点,极大值为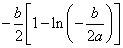 . .
(责任编辑:admin)
|
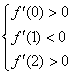 即
即 .
.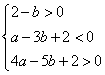 .
.

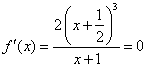 有两个相同的解
有两个相同的解
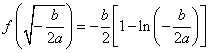 .
.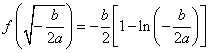 .综上所述,
.综上所述,
