高中学习网-人民教育出版社人教版部编同步解析与测评答案-电子课本资料下载-知识点学习方法与技巧补课解题技巧学习计划表总结-人教网-高中试卷网题库网-中学学科网

首页 > 高中数学B版 > 综合辅导 >

北京第八中学必修1结业测试

http://www.newdu.com 2025/05/18 05:05:01 人民教育出版社 佚名 参加讨论

    西城教育研修学院中学数学室供稿  
    年级:高一  科目: 数学  班级_________ 学号_________ 姓名_________
    一. 选择题 (每题4分, 共48分)
    1. 下列关系式正确的是(      )
    A. Æ Î {2008}             B. Î Q                   C. {2, 3} = {3, 2}         D. {x | x2 = 3x} = {3}
    2. 下列四个图形中，不是以x为自变量的函数的图象是(      )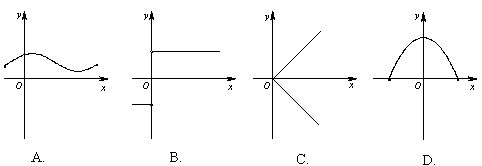
    
    3. 函数的定义域为{0, 1, 2, 3}, 则其值域为(      )
    A. {-1, 0, 3}                B. {0, 1, 2, 3}              C. {y | -1 £ y £ 3}        D. {y | 0 £ y £ 3}
    4. 设、、，则、、的大小关系是(       )
    A.                   B.                   C.                   D.
    5. 设集合S = {y | y = 3x, xÎR}, T = {y | y = x2 - 1, xÎR}, 则S∩T是(      )
    A. Æ                            B. T                             C. S                             D. 有限集
    6. 在同一坐标系中与的图象之间的关系是(      )
    A. 关于y轴对称          B. 关于x轴对称          C. 关于原点对称          D.关于直线y=x对称
    7. 函数的递增区间是(      )
    A. (-∞, -2]                  B. [-5, -2]                   C. [-2, 1]                     D. R
    8. 下列函数中既是奇函数, 又在 (0, +∞)上单调递增的是(      )
    A. y = x2                       B.                  C.                      D.
    9. 函数的图象一定(      )
    A. 关于点 (-2, 3) 对称                                    B. 关于点 (2, -3) 对称
    C. 关于直线x = -2对称                                  D. 关于直线y = -3 对称
    10. 已知 1 < n < m, 下列不等式中正确的的是(      )
    A. m2 < n2            B.             C.          D.
    11. 匀速地向下部是球形, 上部是圆柱形的容器(如右图所示)内注水, 那么注水
    时间t与容器内水的高度h之间的函数关系 h = f(t)的图象大致是下图中的(      )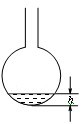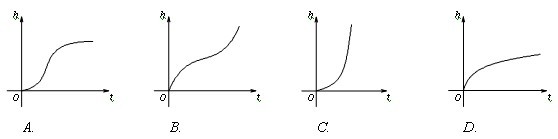
    
    
    12. 定义在N上的函数是增函数，则系数的取值范围是(        )
    A.                       B.                        C.                       D.
    二. 填空题 (每题4分, 共24分)
    13. 已知一次函数f(x)满足 , 则f(x) = _________________________________
    14. 设，则________________
    15. 函数的定义域是________________________
    16. 函数，的值域是______________________
    17. 若，当时，的最大值是________________
    18. 设偶函数在区间上单调递增，且，则这个函数的一个可能的解析式为_____________________________
    三. 解答题 (共48分)
    19. (本题8分)
    已知集合A ={ 6，8，10，12 }，B = {1，6，8}.
    (1) 求A∪B;
    (2) 写出集合A∩B的所有子集.
    20. (本题8分)
    已知y = f(x)是R上的奇函数, 当x > 0时, f(x) = , 求f(x) 在R上的解析式.
    21. (本题10分)
    已知二次函数f(x)满足, 又 f(0) = 3,  f(2) = 1.
    (1) 求函数f(x)的解析式;
    (2) 若f(x) 在[0, m] 上的最大值为3, 最小值为1, 求m的取值范围.
    
    22. (本题10分)
    已知函数  (aÎR)
    (1) 试给出a的一个值, 并画出此时函数的图象;
    (2) 若函数 f (x) 在 R 上具有单调性, 求 a 的取值范围.
    
    23. (本题12分)
    已知f(x)是定义在[-1, 1]上的奇函数, 且f(1) = 1, 若m、nÎ[-1, 1], m+n ¹ 0,  
    (1) 用定义证明: f(x)在[-1, 1]上是增函数;
    (2) 解不等式:
    (3) 若f(x) £ t2 - 2at + 1 对所有 xÎ[-1, 1], aÎ[-1, 1]恒成立, 求实数t的范围
    
    2007—2008学年度第一学期期中测试题
    高一数学答案
    一. 选择题(每题4分, 共48分)
    1. C
    2. C
    3. A
    4. D
    5. C
    6. B
    7. B
    8. D
    9. A
    10. C
    11. B
    12. A
    二. 填空题(每题4分, 共24分)
    13. f(x) = 2x - 或
    14.   1
    15. {x | 2 £ x < 4 且x ¹ 3}
    16.
    17.   1
    18.答案不唯一，如，
    三. 解答题
    19. (8分)(1) A∪B =｛6，8，10，12｝∪｛1，6，8｝=｛1，6，8，10，12｝
    (2) A∩B =｛6，8｝，A∩B的所有子集是，｛6｝，｛8｝，｛6，8｝.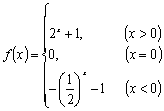 
    20. (8分)
    21. (10分) (1);   
        (2) mÎ[2, 4]
    22. (10分) (1) 图略
    (2) 化简 
    ① a >1时，
    当x ³ -1时，是增函数，且；当x < -1时，是增函数，且.
    所以，当a >1时，函数f (x) 在R上是增函数.
    同理可知，当a <-1时，函数f (x) 在R上是减函数.
    ② a =1或-1时，易知，不合题意.
    ③ -1< a <1时，取x = 0，得f (0) =1，取x =，由< -1，知f () =1，
    所以f (0) = f ().
    所以函数f (x) 在R上不具有单调性.
    综上可知，a的取值范围是.
    23. (12分) (1) 证明略.
    (2)
    (3) (-∞, -2]∪[2, +∞)∪{0}
    八中期中数学考试_必修1结业.zip (责任编辑：admin)



    最近关注
    热点内容