2007年高考数学试题分类汇编——导数(二)
http://www.newdu.com 2025/12/23 04:12:09 人民教育出版社 佚名 参加讨论
23、(福建理 22)已知函数 (Ⅰ)若 (Ⅱ)若 (Ⅲ)设函数 【解答】本小题主要考查函数的单调性、极值、导数、不等式等基本知识,考查运用导数研究函数性质的方法,考查分类讨论、化归以及数形结合等数学思想方法,考查分析问题、解决问题的能力.满分14分. (Ⅰ)由 由 由 (Ⅱ)由 于是 由 ①当 此时 故 ②当 当
由此可得,在 依题意, 综合①,②得,实数 (Ⅲ) 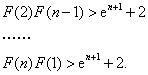 由此得, 故 24、(福建文 20)设函数 (Ⅰ)求 (Ⅱ)若 【解答】本题主要考查函数的单调性、极值以及函数导数的应用,考查运用数学知识分析问题解决问题的能力.满分12分. (Ⅰ) 即 (Ⅱ)令 由 当
即等价于 所以 25、(广东理、文 20)已知 【解答】若 令 当 当 当  或 或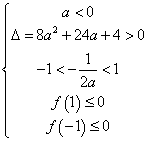 解得 因此 26、(海南理 21)设函数 (I)若当 (II)若 【解答】(Ⅰ) 依题意有 从而 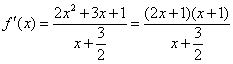 . .当 当 从而, (Ⅱ) 方程 (ⅰ)若 (ⅱ)若 若 当 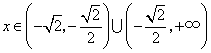 时, 时,若 (ⅲ)若 当 当 综上, 27、(海南文 19)设函数 (Ⅰ)讨论 (Ⅱ)求 【解答】 (Ⅰ) 当 从而, (Ⅱ)由(Ⅰ)知 又 所以 28、(湖北理 20)已知定义在正实数集上的函数 (I)用 (II)求证: 【解答】本小题主要考查函数、不等式和导数的应用等知识,考查综合运用数学知识解决问题的能力. (Ⅰ)设 即 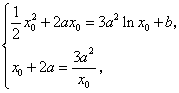 由 由即有 令 当 当 故 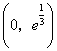 为增函数,在 为增函数,在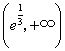 为减函数, 为减函数,于是  . .(Ⅱ)设 则 故 于是函数 故当 29、(湖北文 19)设二次函数 (I)求实数 (II)试比较 【解答】本小题主要考查二次函数、二次方程的基本性质及二次不等式的解法,考查推理和运算能力. 解法1:(Ⅰ)令 则由题意可得 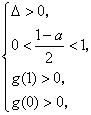  故所求实数 (II) 解法2:(I)同解法1. (II) 即 解法3:(I)方程 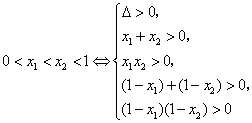 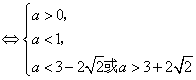 故所求实数 (II)依题意可设 (责任编辑:admin) |