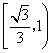37、(江西理)设椭圆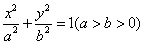 的离心率为 的离心率为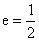 ,右焦点为 ,右焦点为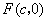 ,方程 ,方程 的两个实根分别为 的两个实根分别为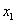 和 和 ,则点 ,则点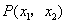 ( ) ( )
A.必在圆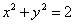 内 B.必在圆 内 B.必在圆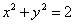 上 上
C.必在圆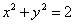 外 D.以上三种情形都有可能 外 D.以上三种情形都有可能
【解答】由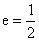 = =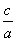 得a=2c,b= 得a=2c,b= ,所以 ,所以 ,所以点 ,所以点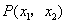 到圆心(0,0)的距离为 到圆心(0,0)的距离为 ,所以点P在圆内,选A ,所以点P在圆内,选A
38、(江西理)(本小题满分12分)设动点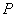 到点 到点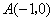 和 和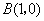 的距离分别为 的距离分别为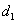 和 和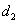 , ,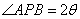 ,且存在常数 ,且存在常数 ,使得 ,使得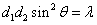 . .
(1)证明:动点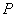 的轨迹 的轨迹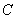 为双曲线,并求出 为双曲线,并求出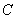 的方程; 的方程;
(2)过点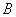 作直线双曲线 作直线双曲线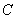 的右支于 的右支于 两点,试确定 两点,试确定 的范围,使 的范围,使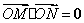 ,其中点 ,其中点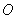 为坐标原点. 为坐标原点.

【解答】解法一:(1)在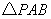 中, 中,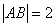 ,即 ,即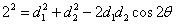 , ,
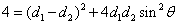 ,即 ,即 (常数), (常数),
点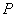 的轨迹 的轨迹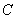 是以 是以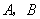 为焦点,实轴长 为焦点,实轴长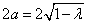 的双曲线. 的双曲线.
方程为: . .
(2)设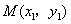 , ,
①当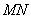 垂直于 垂直于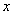 轴时, 轴时,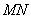 的方程为 的方程为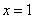 , ,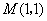 , ,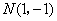 在双曲线上. 在双曲线上.
即 ,因为 ,因为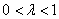 ,所以 ,所以 . .
②当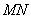 不垂直于 不垂直于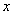 轴时,设 轴时,设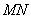 的方程为 的方程为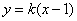 . .
由 得: 得: , ,
由题意知: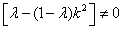 , ,
所以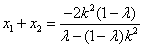 , , . .
于是: . .
因为 ,且 ,且 在双曲线右支上,所以 在双曲线右支上,所以
 . .
由①②知, . .
解法二:(1)同解法一
(2)设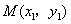 , , , ,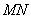 的中点为 的中点为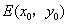 . .
①当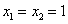 时, 时,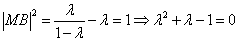 , ,
因为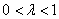 ,所以 ,所以 ; ;
②当 时, 时,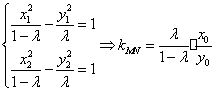 . .
又 .所以 .所以 ; ;
由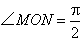 得 得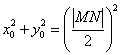 ,由第二定义得 ,由第二定义得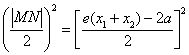
 . .
所以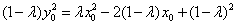 . .
于是由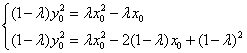 得 得
因为 ,所以 ,所以 ,又 ,又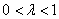 , ,
解得: .由①②知 .由①②知 . .
39、(江西文)连接抛物线 的焦点 的焦点 与点 与点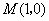 所得的线段与抛物线交于点 所得的线段与抛物线交于点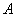 ,设点 ,设点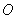 为坐标原点,则三角形 为坐标原点,则三角形 的面积为( ) 的面积为( )
A.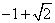 B. B.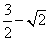 C. C.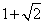 D. D.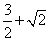
【解答】线段 所在直线方程 所在直线方程 与抛物线交于 与抛物线交于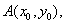 则: 则:
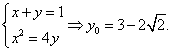 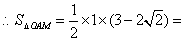 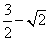 ,选B ,选B
40、(江西文)设椭圆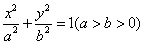 的离心率为 的离心率为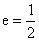 ,右焦点为 ,右焦点为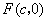 ,方程 ,方程 的两个实根分别为 的两个实根分别为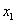 和 和 ,则点 ,则点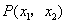 ( ) ( )
A.必在圆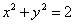 上 B.必在圆 上 B.必在圆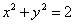 外 外
C.必在圆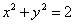 内 D.以上三种情形都有可能 内 D.以上三种情形都有可能
【解答】由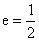 = =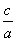 得a=2c,b= 得a=2c,b= ,所以 ,所以 , ,
所以点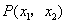 到圆心(0,0)的距离为 到圆心(0,0)的距离为
 , ,
所以点P在圆内,选C.
41、(江西文)(本小题满分14分)设动点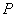 到点 到点 和 和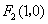 的距离分别为 的距离分别为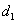 和 和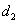 , ,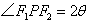 ,且存在常数 ,且存在常数 ,使得 ,使得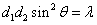 . .
(1)证明:动点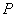 的轨迹 的轨迹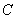 为双曲线,并求出 为双曲线,并求出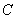 的方程; 的方程;
(2)如图,过点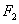 的直线与双曲线 的直线与双曲线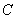 的右支交于 的右支交于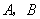 两点.问:是否存在 两点.问:是否存在 ,使 ,使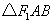 是以点 是以点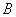 为直角顶点的等腰直角三角形?若存在,求出 为直角顶点的等腰直角三角形?若存在,求出 的值;若不存在,说明理由. 的值;若不存在,说明理由.
 
【解答】(1)在 中, 中,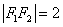
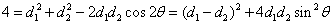

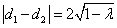 (小于 (小于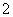 的常数) 的常数)
故动点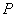 的轨迹 的轨迹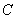 是以 是以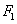 , ,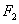 为焦点,实轴长 为焦点,实轴长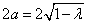 的双曲线. 的双曲线.
方程为 . .
(2)方法一:在 中,设 中,设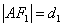 , ,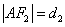 , ,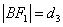 , ,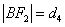 . .
假设 为等腰直角三角形,则 为等腰直角三角形,则

由②与③得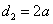 , ,
则
由⑤得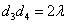 , ,
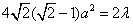
 , ,
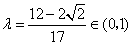
故存在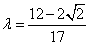 满足题设条件. 满足题设条件.
方法二:(1)设 为等腰直角三角形,依题设可得 为等腰直角三角形,依题设可得

所以 , ,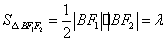 . .
则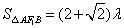 .① .①
由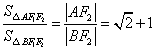 ,可设 ,可设 , ,
则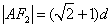 , , . .
则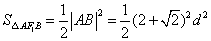 .② .②
由①②得 .③ .③
根据双曲线定义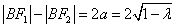 可得, 可得, . .
平方得: .④ .④
由③④消去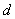 可解得, 可解得,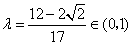
故存在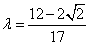 满足题设条件. 满足题设条件.
42、(江苏理)在平面直角坐标系 中,双曲线中心在原点,焦点在 中,双曲线中心在原点,焦点在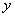 轴上,一条渐近线方程为 轴上,一条渐近线方程为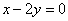 ,则它的离心率为 ,则它的离心率为
A.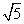 B. B. C. C.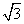 D. D.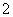
【解答】由  , ,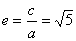 选A 选A
43、(江苏理)在平面直角坐标系 中,已知 中,已知 顶点 顶点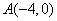 和 和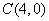 ,顶点 ,顶点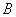 在椭圆 在椭圆 上,则 上,则 . .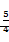
【解答】利用椭圆定义和正弦定理 得  b=2*4=8 b=2*4=8
 
44、(江苏理)(本小题满分14分)如图,在平面直角坐标系 中,过 中,过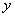 轴正方向上一点 轴正方向上一点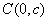 任作一直线,与抛物线 任作一直线,与抛物线 相交于 相交于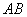 两点,一条垂直于 两点,一条垂直于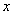 轴的直线,分别与线段 轴的直线,分别与线段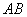 和直线 和直线 交于 交于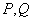 , ,
(1)若 ,求 ,求 的值;(5分) 的值;(5分)
(2)若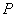 为线段 为线段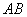 的中点,求证: 的中点,求证: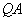 为此抛物线的切线;(5分) 为此抛物线的切线;(5分)
(3)试问(2)的逆命题是否成立?说明理由。(4分)
 
【解答】(1)设过C点的直线为 ,所以 ,所以 ,即 ,即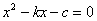 ,设A ,设A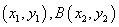 , , = =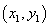 , , ,因为 ,因为 ,所以 ,所以
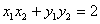 ,即 ,即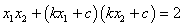 , ,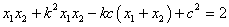
所以 ,即 ,即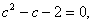 所以 所以
(2)设过Q的切线为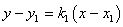 , ,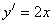 ,所以 ,所以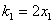 ,即 ,即 ,它与 ,它与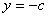 的交点为M 的交点为M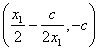 ,又 ,又 ,所以Q ,所以Q ,因为 ,因为 ,所以 ,所以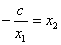 ,所以M ,所以M ,所以点M和点Q重合,也就是QA为此抛物线的切线。 ,所以点M和点Q重合,也就是QA为此抛物线的切线。
(3)(2)的逆命题是成立,由(2)可知Q ,因为PQ ,因为PQ 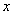 轴,所以 轴,所以
因为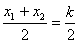 ,所以P为AB的中点。 ,所以P为AB的中点。
45、(湖南理)设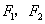 分别是椭圆 分别是椭圆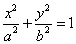 ( (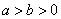 )的左、右焦点,若在其右准线上存在 )的左、右焦点,若在其右准线上存在 使线段 使线段 的中垂线过点 的中垂线过点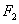 ,则椭圆离心率的取值范围是( ) ,则椭圆离心率的取值范围是( )
A. B. B. C. C.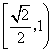 D. D.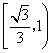
【解答】由已知P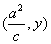 ,所以 ,所以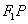 的中点Q的坐标为 的中点Q的坐标为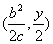 ,由 ,由
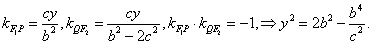

当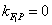 时, 时,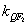 不存在,此时 不存在,此时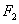 为中点, 为中点,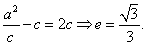
综上得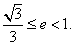
(责任编辑:admin)
|

 得:
得: .
.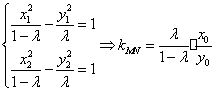 .
.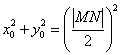 ,由第二定义得
,由第二定义得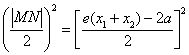
 .
.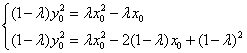 得
得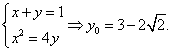





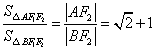 ,可设
,可设

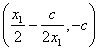 ,又
,又 ,所以Q
,所以Q B.
B. C.
C.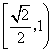 D.
D.