22、(山东理)(本小题满分12分)已知椭圆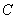 的中心在坐标原点,焦点在 的中心在坐标原点,焦点在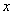 轴上,椭圆 轴上,椭圆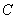 上的点到焦点距离的最大值为 上的点到焦点距离的最大值为 ,最小值为 ,最小值为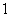 . .
(Ⅰ)求椭圆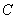 的标准方程; 的标准方程;
(Ⅱ)若直线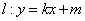 与椭圆 与椭圆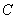 相交于 相交于 , ,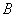 两点( 两点( 不是左右顶点),且以 不是左右顶点),且以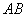 为直径的圆过椭圆 为直径的圆过椭圆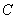 的右顶点,求证:直线 的右顶点,求证:直线 过定点,并求出该定点的坐标. 过定点,并求出该定点的坐标.
【解答】(I)由题意设椭圆的标准方程为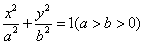
 , ,
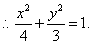
(II)设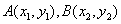 ,由 ,由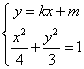 得 得
 , ,
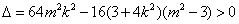 , ,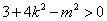 . .
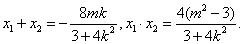
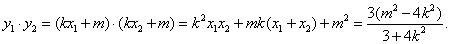
 以AB为直径的圆过椭圆的右顶点 以AB为直径的圆过椭圆的右顶点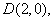  , ,
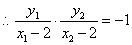 , ,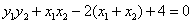 , ,
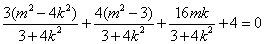 , ,
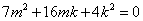 ,解得 ,解得
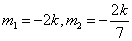 ,且满足 ,且满足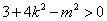 . .
当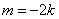 时, 时, ,直线过定点 ,直线过定点 与已知矛盾; 与已知矛盾;
当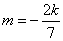 时, 时,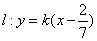 ,直线过定点 ,直线过定点
综上可知,直线 过定点,定点坐标为 过定点,定点坐标为
23、(全国2理)设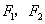 分别是双曲线 分别是双曲线 的左、右焦点,若双曲线上存在点 的左、右焦点,若双曲线上存在点 ,使 ,使 且 且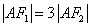 ,则双曲线的离心率为( B ) ,则双曲线的离心率为( B )
A.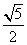 B. B. C. C.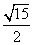 D. D.
【解答】设F1,F2分别是双曲线 的左、右焦点。若双曲线上存在点A,使∠F1AF2=90º,且|AF1|=3|AF2|,设|AF2|=1,|AF1|=3,双曲线中 的左、右焦点。若双曲线上存在点A,使∠F1AF2=90º,且|AF1|=3|AF2|,设|AF2|=1,|AF1|=3,双曲线中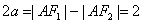 , ,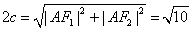 ,∴ 离心率 ,∴ 离心率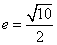 ,选B。 ,选B。
24、(全国2理)设 为抛物线 为抛物线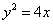 的焦点, 的焦点, 为该抛物线上三点,若 为该抛物线上三点,若 ,则 ,则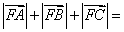 ( ) ( )
A.9 B.6 C.4 D.3
【解答】设F为抛物线y2=4x的焦点,A、B、C为该抛物线上三点,若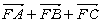 =0,则F为△ABC的重心,∴ A、B、C三点的横坐标的和为F点横坐标的3倍,即等于3, =0,则F为△ABC的重心,∴ A、B、C三点的横坐标的和为F点横坐标的3倍,即等于3,
∴ |FA|+|FB|+|FC|=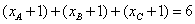 ,选B。 ,选B。
25、(全国2理)(本小题满分12分)在直角坐标系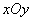 中,以 中,以 为圆心的圆与直线 为圆心的圆与直线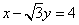 相切. 相切.
(1)求圆 的方程; 的方程;
(2)圆 与 与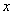 轴相交于 轴相交于 两点,圆内的动点 两点,圆内的动点 使 使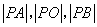 成等比数列,求 成等比数列,求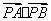 的取值范围. 的取值范围.
【解答】(1)依题设,圆 的半径 的半径 等于原点 等于原点 到直线 到直线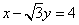 的距离, 的距离,
即 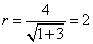 . .
得圆 的方程为 的方程为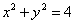 . .
(2)不妨设 .由 .由 即得 即得
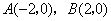 . .
设 ,由 ,由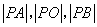 成等比数列,得 成等比数列,得
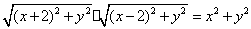 , ,
即 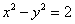 . .


由于点 在圆 在圆 内,故 内,故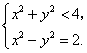
由此得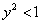 . .
所以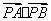 的取值范围为 的取值范围为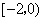 . .
26、(全国2文)已知椭圆的长轴长是短轴长的2倍,则椭圆的离心率等于( )
A. B. B. C. C. D. D.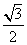
【解答】已知椭圆的长轴长是短轴长的2倍,∴ 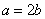 ,椭圆的离心率 ,椭圆的离心率 ,选D。 ,选D。
27、(全国2文)设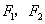 分别是双曲线 分别是双曲线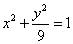 的左、右焦点.若点 的左、右焦点.若点 在双曲线上,且 在双曲线上,且 ,则 ,则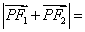 ( ) ( )
A.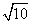 B. B. C. C. D. D.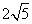
【解答】设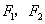 分别是双曲线 分别是双曲线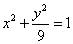 的左、右焦点.若点 的左、右焦点.若点 在双曲线上,且 在双曲线上,且 ,则 ,则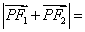 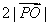 = =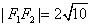 ,选B。 ,选B。
28、(全国1理)已知双曲线的离心率为 ,焦点是 ,焦点是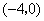 , , ,则双曲线方程为( ) ,则双曲线方程为( )
A.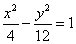 B. B.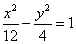 C. C. D. D.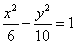
【解答】已知双曲线的离心率为2,焦点是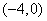 , ,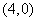 ,则c=4,a=2, ,则c=4,a=2, ,双曲线方程为 ,双曲线方程为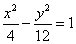 ,选A。 ,选A。
29、(全国1理)抛物线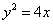 的焦点为 的焦点为 ,准线为 ,准线为 ,经过 ,经过 且斜率为 且斜率为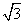 的直线与抛物线在 的直线与抛物线在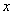 轴上方的部分相交于点 轴上方的部分相交于点 , ,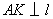 ,垂足为 ,垂足为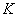 ,则 ,则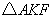 的面积是( ) 的面积是( )
A. B. B.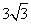 C. C.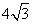 D. D.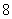
【解答】抛物线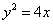 的焦点F(1,0),准线为l: 的焦点F(1,0),准线为l: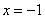 ,经过F且斜率为 ,经过F且斜率为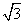 的直线 的直线 与抛物线在x轴上方的部分相交于点A(3,2 与抛物线在x轴上方的部分相交于点A(3,2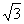 ), ),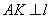 ,垂足为K(-1,2 ,垂足为K(-1,2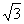 ),∴ △AKF的面积是4 ),∴ △AKF的面积是4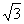 ,选C。 ,选C。
30、(全国1理)(本小题满分12分)已知椭圆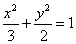 的左、右焦点分别为 的左、右焦点分别为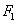 , ,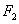 .过 .过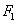 的直线交椭圆于 的直线交椭圆于 两点,过 两点,过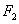 的直线交椭圆于 的直线交椭圆于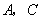 两点,且 两点,且 ,垂足为 ,垂足为 . .
(Ⅰ)设 点的坐标为 点的坐标为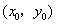 ,证明: ,证明: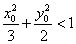 ; ;
(Ⅱ)求四边形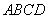 的面积的最小值. 的面积的最小值.
【解答】(Ⅰ)证明:椭圆的半焦距 , ,
由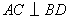 知点 知点 在以线段 在以线段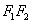 为直径的圆上,故 为直径的圆上,故 , ,
所以,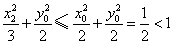 . .
(Ⅱ)(ⅰ)当 的斜率 的斜率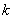 存在且 存在且 时, 时, 的方程为 的方程为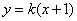 ,代入椭圆方程 ,代入椭圆方程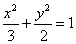 ,并化简得 ,并化简得 . .
设 , ,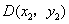 ,则 ,则
 , ,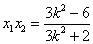
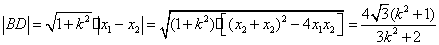 ; ;
因为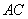 与 与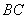 相交于点 相交于点 ,且 ,且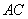 的斜率为 的斜率为 , ,
所以, . .
四边形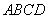 的面积 的面积
 . .
当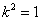 时,上式取等号. 时,上式取等号.
(ⅱ)当 的斜率 的斜率 或斜率不存在时,四边形 或斜率不存在时,四边形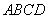 的面积 的面积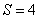 . .
综上,四边形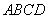 的面积的最小值为 的面积的最小值为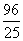 . .
31、(海南、宁夏理)已知抛物线 的焦点为 的焦点为 ,点 ,点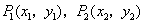 , ,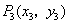 在抛物线上,且 在抛物线上,且 , 则有( C ) , 则有( C )
A. B. B.
C. D. D.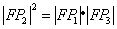
【分析】:由抛物线定义,
 即: 即: . .
32、(海南、宁夏理)已知双曲线的顶点到渐近线的距离为2,焦点到渐近线的距离为6,则该双曲线的离心率为 .3
【分析】:如图,过双曲线的顶点A、焦点F分别向其渐近线作垂线,垂足分别为B、C,则:
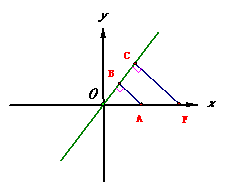
33、(海南、宁夏理)(本小题满分12分)在平面直角坐标系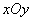 中,经过点 中,经过点 且斜率为 且斜率为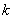 的直线 的直线 与椭圆 与椭圆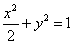 有两个不同的交点 有两个不同的交点 和 和 . .
(I)求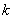 的取值范围; 的取值范围;
(II)设椭圆与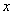 轴正半轴、 轴正半轴、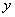 轴正半轴的交点分别为 轴正半轴的交点分别为 ,是否存在常数 ,是否存在常数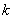 ,使得向量 ,使得向量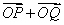 与 与 共线?如果存在,求 共线?如果存在,求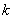 值;如果不存在,请说明理由. 值;如果不存在,请说明理由.
【解答】(Ⅰ)由已知条件,直线 的方程为 的方程为 , ,
代入椭圆方程得 . .
整理得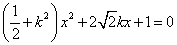 ① ①
直线 与椭圆有两个不同的交点 与椭圆有两个不同的交点 和 和 等价于 等价于 , ,
解得 或 或 .即 .即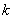 的取值范围为 的取值范围为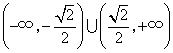 . .
(Ⅱ)设 ,则 ,则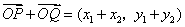 , ,
由方程①, . ② . ②
又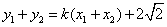 . ③ . ③
而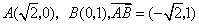 . .
所以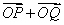 与 与 共线等价于 共线等价于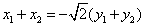 , ,
将②③代入上式,解得 . .
由(Ⅰ)知 或 或 ,故没有符合题意的常数 ,故没有符合题意的常数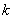 . .
34、(辽宁理)设 为双曲线 为双曲线 上的一点, 上的一点,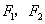 是该双曲线的两个焦点,若 是该双曲线的两个焦点,若 ,则 ,则 的面积为( ) 的面积为( )
A.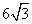 B. B.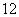 C. C. D. D.
【解答】因为 ,设 ,设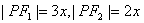 ,根据双曲线定义得 ,根据双曲线定义得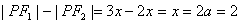 ,所以 ,所以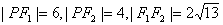 , , , , 为直角三角形,其面积为 为直角三角形,其面积为 ,选B ,选B
35、(辽宁理)设椭圆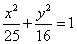 上一点 上一点 到左准线的距离为10, 到左准线的距离为10, 是该椭圆的左焦点,若点 是该椭圆的左焦点,若点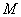 满足 满足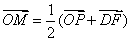 ,则 ,则 = . = .
【解答】椭圆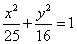 左准线为 左准线为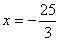 ,左焦点为(-3,0),P( ,左焦点为(-3,0),P(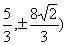 ,由已知M为PF中点,M( ,由已知M为PF中点,M(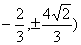 ,所以 ,所以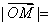 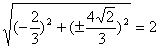
36、(辽宁理)(本小题满分14分)已知正三角形 的三个顶点都在抛物线 的三个顶点都在抛物线 上,其中 上,其中 为坐标原点,设圆 为坐标原点,设圆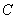 是 是 的内接圆(点 的内接圆(点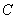 为圆心) 为圆心)
(I)求圆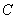 的方程; 的方程;
(II)设圆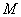 的方程为 的方程为 ,过圆 ,过圆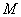 上任意一点 上任意一点 分别作圆 分别作圆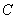 的两条切线 的两条切线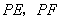 ,切点为 ,切点为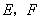 ,求 ,求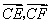 的最大值和最小值. 的最大值和最小值.
【解答】本小题主要考查平面向量,圆与抛物线的方程及几何性质等基本知识,考查综合运用解析几何知识解决问题的能力.满分14分.
(I)解法一:设 两点坐标分别为 两点坐标分别为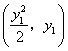 , , ,由题设知 ,由题设知
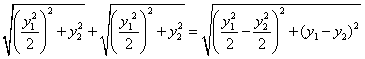 . .
解得 , ,
所以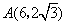 , ,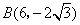 或 或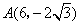 , , . .
设圆心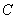 的坐标为 的坐标为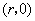 ,则 ,则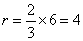 ,所以圆 ,所以圆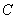 的方程为 的方程为
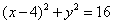 .················ 4分 .················ 4分
解法二:设 两点坐标分别为 两点坐标分别为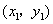 , ,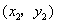 ,由题设知 ,由题设知
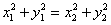 . .
又因为 , , ,可得 ,可得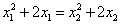 .即 .即
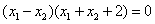 . .
由 , ,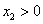 ,可知 ,可知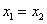 ,故 ,故 两点关于 两点关于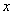 轴对称,所以圆心 轴对称,所以圆心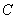 在 在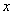 轴上. 轴上.
设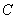 点的坐标为 点的坐标为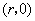 ,则 ,则 点坐标为 点坐标为 ,于是有 ,于是有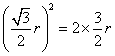 ,解得 ,解得 ,所以圆 ,所以圆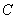 的方程为 的方程为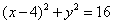 .···· 4分 .···· 4分
(II)解:设 ,则 ,则
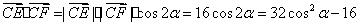 .········ 8分 .········ 8分
在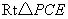 中, 中,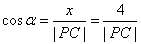 ,由圆的几何性质得 ,由圆的几何性质得
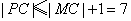  , , , ,
所以 ,由此可得 ,由此可得
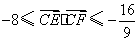 . .
则 的最大值为 的最大值为 ,最小值为 ,最小值为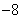 . .
(责任编辑:admin)
|
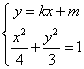 得
得
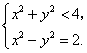
 .
. .
.
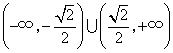 .
.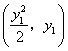 ,
, ,由题设知
,由题设知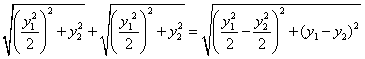 .
. ,于是有
,于是有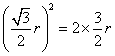 ,解得
,解得