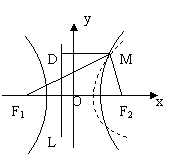
46、(本小题满分12分)已知双曲线 的左、右焦点分别为 的左、右焦点分别为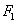 , ,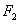 ,过点 ,过点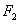 的动直线与双曲线相交于 的动直线与双曲线相交于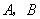 两点. 两点.
(I)若动点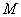 满足 满足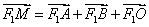 (其中 (其中 为坐标原点),求点 为坐标原点),求点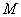 的轨迹方程; 的轨迹方程;
(II)在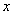 轴上是否存在定点 轴上是否存在定点 ,使 ,使 · ·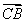 为常数?若存在,求出点 为常数?若存在,求出点 的坐标;若不存在,请说明理由. 的坐标;若不存在,请说明理由.
【解答】由条件知 , ,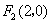 ,设 ,设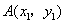 , , . .
解法一:(I)设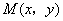 ,则 ,则 则 则 , , , ,
 ,由 ,由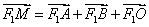 得 得
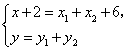 即 即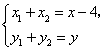
于是 的中点坐标为 的中点坐标为 . .
当 不与 不与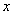 轴垂直时, 轴垂直时,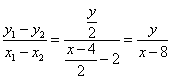 ,即 ,即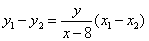 . .
又因为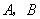 两点在双曲线上,所以 两点在双曲线上,所以 , , ,两式相减得 ,两式相减得
 ,即 ,即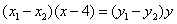 . .
将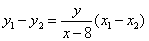 代入上式,化简得 代入上式,化简得 . .
当 与 与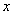 轴垂直时, 轴垂直时,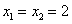 ,求得 ,求得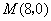 ,也满足上述方程. ,也满足上述方程.
所以点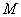 的轨迹方程是 的轨迹方程是 . .
(II)假设在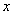 轴上存在定点 轴上存在定点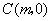 ,使 ,使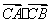 为常数. 为常数.
当 不与 不与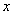 轴垂直时,设直线 轴垂直时,设直线 的方程是 的方程是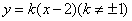 . .
代入 有 有 . .
则 是上述方程的两个实根,所以 是上述方程的两个实根,所以 , , , ,
于是
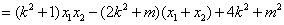
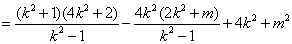
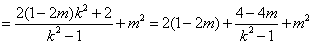 . .
因为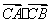 是与 是与 无关的常数,所以 无关的常数,所以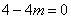 ,即 ,即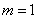 ,此时 ,此时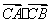 = = . .
当 与 与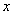 轴垂直时,点 轴垂直时,点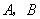 的坐标可分别设为 的坐标可分别设为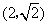 , ,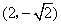 , ,
此时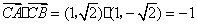 . .
故在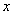 轴上存在定点 轴上存在定点 ,使 ,使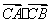 为常数. 为常数.
解法二:(I)同解法一的(I)有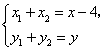
当 不与 不与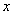 轴垂直时,设直线 轴垂直时,设直线 的方程是 的方程是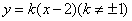 . .
代入 有 有 . .
则 是上述方程的两个实根,所以 是上述方程的两个实根,所以 . .
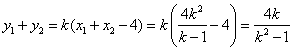 . .
由①②③得 .…………………④ .…………………④
 .……………………………⑤ .……………………………⑤
当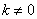 时, 时,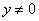 ,由④⑤得, ,由④⑤得,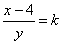 ,将其代入⑤有 ,将其代入⑤有
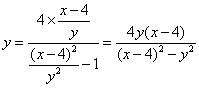 .整理得 .整理得 . .
当 时,点 时,点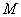 的坐标为 的坐标为 ,满足上述方程. ,满足上述方程.
当 与 与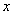 轴垂直时, 轴垂直时,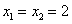 ,求得 ,求得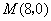 ,也满足上述方程. ,也满足上述方程.
故点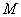 的轨迹方程是 的轨迹方程是 . .
(II)假设在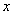 轴上存在定点点 轴上存在定点点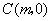 ,使 ,使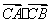 为常数, 为常数,
当 不与 不与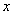 轴垂直时,由(I)有 轴垂直时,由(I)有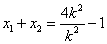 , , . .
以上同解法一的(II).
47、(湖南文)设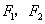 分别是椭圆 分别是椭圆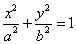 ( (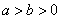 )的左、右焦点, )的左、右焦点,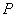 是其右准线上纵坐标为 是其右准线上纵坐标为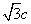 ( ( 为半焦距)的点,且 为半焦距)的点,且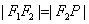 ,则椭圆的离心率是( ) ,则椭圆的离心率是( )
A.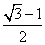 B. B. C. C. D. D.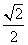
【解答】由已知P( ),所以 ),所以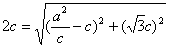 化简得 化简得
48、(湖南文)(本小题满分13分)已知双曲线 的右焦点为 的右焦点为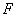 ,过点 ,过点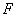 的动直线与双曲线相交于 的动直线与双曲线相交于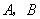 两点,点 两点,点 的坐标是 的坐标是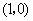 . .
(I)证明 , ,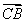 为常数; 为常数;
(II)若动点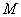 满足 满足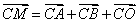 (其中 (其中 为坐标原点),求点 为坐标原点),求点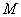 的轨迹方程. 的轨迹方程.
【解答】由条件知 ,设 ,设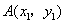 , , . .
(I)当 与 与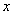 轴垂直时,可设点 轴垂直时,可设点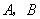 的坐标分别为 的坐标分别为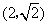 , ,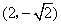 , ,
此时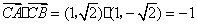 . .
当 不与 不与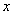 轴垂直时,设直线 轴垂直时,设直线 的方程是 的方程是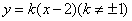 . .
代入 ,有 ,有 . .
则 是上述方程的两个实根,所以 是上述方程的两个实根,所以 , , , ,
于是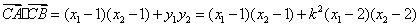
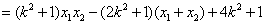
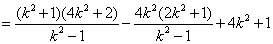
 . .
综上所述,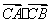 为常数 为常数 . .
(II)解法一:设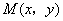 ,则 ,则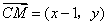 , ,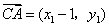 , ,
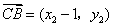 , ,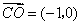 ,由 ,由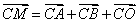 得: 得:
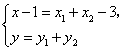 即 即
于是 的中点坐标为 的中点坐标为 . .
当 不与 不与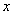 轴垂直时, 轴垂直时,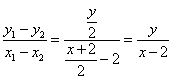 ,即 ,即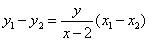 . .
又因为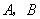 两点在双曲线上,所以 两点在双曲线上,所以 , , ,两式相减得 ,两式相减得
 ,即 ,即 . .
将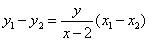 代入上式,化简得 代入上式,化简得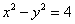 . .
当 与 与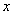 轴垂直时, 轴垂直时,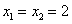 ,求得 ,求得 ,也满足上述方程. ,也满足上述方程.
所以点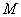 的轨迹方程是 的轨迹方程是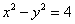 . .
解法二:同解法一得 ……………………① ……………………①
当 不与 不与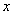 轴垂直时,由(I) 有 轴垂直时,由(I) 有 .……………② .……………②
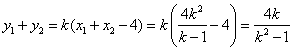 .………………③ .………………③
由①②③得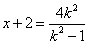 .…………………………④ .…………………………④
 .…………………………………⑤ .…………………………………⑤
当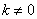 时, 时,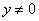 ,由④⑤得, ,由④⑤得,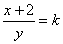 ,将其代入⑤有 ,将其代入⑤有
 .整理得 .整理得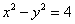 . .
当 时,点 时,点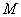 的坐标为 的坐标为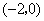 ,满足上述方程. ,满足上述方程.
当 与 与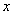 轴垂直时, 轴垂直时,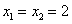 ,求得 ,求得 ,也满足上述方程. ,也满足上述方程.
故点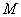 的轨迹方程是 的轨迹方程是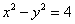 . .
49、(湖北理)双曲线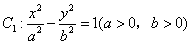 的左准线为 的左准线为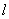 ,左焦点和右焦点分别为 ,左焦点和右焦点分别为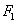 和 和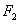 ;抛物线 ;抛物线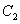 的准线为 的准线为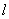 ,焦点为 ,焦点为 与 与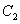 的一个交点为 的一个交点为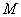 ,则 ,则 等于( ) 等于( )
A. B. B.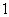 C. C. D. D.
【解答】由题设可知点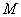 同时满足双曲线和抛物线的定义,且在双曲线右支上,故 由定义可得 同时满足双曲线和抛物线的定义,且在双曲线右支上,故 由定义可得
 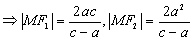
故原式 ,选A ,选A
点评:本题主要考察双曲线和抛物线的定义和性质,几何条件列方程组,消元后化归曲线的基本量的计算,体现数形结合方法的重要性。
易错点:由于畏惧心理而胡乱选择,不能将几何条件有机联系转化,缺乏消元意识。
50、(湖北理)已知直线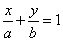 ( ( 是非零常数)与圆 是非零常数)与圆 有公共点,且公共点的横坐标和纵坐标均为整数,那么这样的直线共有( ) 有公共点,且公共点的横坐标和纵坐标均为整数,那么这样的直线共有( )
A.60条 B.66条 C.72条 D.78条
【解答】可知直线的横、纵截距都不为零,即与坐标轴不垂直,不过坐标原点,而圆 上的整数点共有12个,分别为 上的整数点共有12个,分别为 , , ,前8个点中,过任意一点的圆的切线满足,有8条;12个点中过任意两点,构成 ,前8个点中,过任意一点的圆的切线满足,有8条;12个点中过任意两点,构成 条直线,其中有4条直线垂直 条直线,其中有4条直线垂直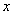 轴,有4条直线垂直 轴,有4条直线垂直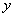 轴,还有6条过原点(圆上点的对称性),故满足题设的直线有52条。综上可知满足题设的直线共有 轴,还有6条过原点(圆上点的对称性),故满足题设的直线有52条。综上可知满足题设的直线共有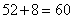 条,选A 条,选A
点评:本题主要考察直线与圆的概念,以及组合的知识,既要数形结合,又要分类考虑,要结合圆上点的对称性来考虑过点的直线的特征。是较难问题
易错点:不能准确理解题意,甚至混淆。对直线截距式方程认识不明确,认识不到三类特殊直线不能用截距式方程表示;对圆上的整数点探索不准确,或分类不明确,都会导致错误,胡乱选择。
(责任编辑:admin)
|
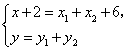 即
即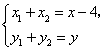
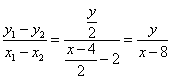 ,即
,即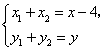
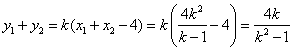 .
.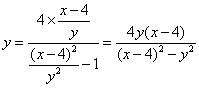 .整理得
.整理得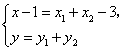 即
即
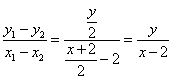 ,即
,即 ……………………①
……………………①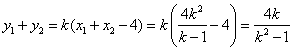 .………………③
.………………③ .整理得
.整理得
 ,选A
,选A
