3.5导数及其运用单元测试
http://www.newdu.com 2025/11/26 07:11:18 人民教育出版社 佚名 参加讨论
3.5导数及其运用单元测试 1、设  是可导函数，且 （ ）A．  B．－1 C．0 D．－22、f/（x）是f（x）的导函数，f/（x）的图象如右图所示，则f（x）的图象只可能是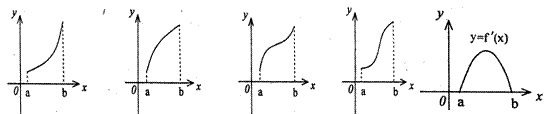（ ）  （A） （B） （C） （D） 3、下列函数中,在  上为增函数的是 （ ）A.  B. C. D. 4、已知  是R上的单调增函数，则 的取值范围是 （ ）A.  B.  C.  D.  5、已知函数  在 上是单调函数,则实数 的取值范围是（ ）A.  B. C.  D.  6、下列说法正确的是 （ ） A. 函数在闭区间上的极大值一定比极小值大; B. 函数在闭区间上的最大值一定是极大值; C. 对于  ,若 ,则无极值;D.函数 在区间 上一定存在最值.7、函数  在 处有极值10, 则点为 （ ）A.  B. C. 或 D.不存在8、定义在闭区间  上的连续函数 有唯一的极值点 ,且 ,则下列说法正确的是 （ ）A.函数 有最小值 B. 函数有最小值,但不一定是C.函数 的最大值也可能是 D. 函数不一定有最小值9、函数  在[0，3]上的最大值和最小值分别是 （ ）A. 5，15 B. 5，  C. 5， D. 5， 10、函数  上最大值等于 （ ）A．  B． C． D． 11、设函数  ，则 ′ ＝____________________12、函数  的单调递减区间为 13、函数  的极大值为6,极小值为2,则的减区间是 14、点  是曲线 上任意一点, 则点到直线 的距离的最小值是 15、已知直线  为曲线 在点 处的切线， 为该曲线的另一条切线，且  （Ⅰ）求直线的方程；（Ⅱ）求由直线 和 轴所围成的三角形的面积 16、设函数  （Ⅰ）当  求函数满足 时的 的集合；（Ⅱ）求a的取值范围，使f（x）在区间（0，+∞）上是单调减函数 17、设函数f(x)=x(x-1)(x-a),(a>1) (Ⅰ)求导数f? (x); (Ⅱ)若不等式f(x1)+ f(x2)?0成立，求a的取值范围 18、已知  在 时有极大值6，在时有极小值，求 的值；并求在区间[－3，3]上的最大值和最小值.19、设函数  （Ⅰ）求 的单调区间和极值；（Ⅱ）若关于 的方程 有3个不同实根，求实数a的取值范围.（Ⅲ）已知当  恒成立，求实数k的取值范围.参考答案： 1.B; 2.D; 3.B; 4.D; 5.B; 6.C; 7.B; 8.A; 9.C; 10.D; 11.  ; 12. ; 13.  ;14. 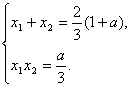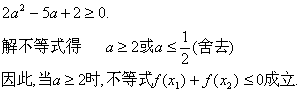;15、(I)解：  令  得 若  则 ，故 在 上是增函数，在 上是增函数 若  则 ，故在 上是减函数 (II)    16、解：（Ⅰ）当  ,化为   故，满足（Ⅰ）条件的集合为  （Ⅱ）  要使f（x）在区间（0，+∞）上是单调减函数，必须  ，即  ，但 时，为常函数，所以 17、.解:（I）  （II）因   又由（I）知  代入前面不等式，两边除以（1+a），并化简得 18、.解：（1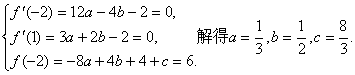）  由条件知 （2） 
由上表知，在区间[－3，3]上，当  时， 时， 19、解:（Ⅰ）  ∴当  ，∴ 的单调递增区间是 ，单调递减区间是 当  ；当 （Ⅱ）由（Ⅰ）的分析可知 图象的大致形状及走向（图略）∴当  的图象有3个不同交点，即方程  有三解（（Ⅲ）  ∵  上恒成立令  ，由二次函数的性质， 上是增函数，∴  ∴所求k的取值范围是 (责任编辑：admin) |
- 上一篇：2.5圆锥曲线单元测试
- 下一篇：2.4抛物线