选修1-1综合测试
http://www.newdu.com 2025/11/30 02:11:24 人民教育出版社 佚名 参加讨论
选修1-1综合测试 1．已知命题甲：  ，命题乙：点 是可导函数 的极值点，则甲是乙的（ ）A．充分而不必要条件 B．必要而不充分条件 C．充要条件 D．既不充分而不必要条件 2、已知椭圆的焦点为  和 ，点 在椭圆上的一点，且 是 的等差中项，则该椭圆的方程为（ ）A、  B、 C、 D、 3、已知  ，点P在A、B所在的平面内运动且保持 ，则 的最大值和最小值分别是 ( )A．  、3 B．10、2 C．5、1 D．6、44、椭圆的一焦点与短轴两顶点组成一个等边三角形，则椭圆的离心率为（ ） A、  B、 C、 D、 5．双曲线x2－ay2＝1的焦点坐标是 （ ） A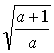．(  , 0) , (－ , 0)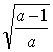 B．( , 0), (－ , 0) C．（－  , 0）,（ , 0） D．(－ , 0), ( , 0)6、若双曲线  与 的离心率分别为 ，则当 变化时， 的最小值是（ ）A．  B． C． D． 7.曲线y=x3+x-2在点P0处的切线平行于直线y=4x-1,则P0的坐标可能是( ) A.(0,1) B.(1,0) C.(-1,0) D.(1,4) 8. 函数  在区间 上单调递增，那么实数a的取值范围是（ ）A．  B． C． D． 9、方程x3－6x2+9x－10=0的实根个数是 （ ） A、3 B、2 C、1 D、0 10．已知函数f(x)的导函数  的图像如左图所示，那么函数f(x)的图像最有可能的是( ) 11．命题  的否命题是 .12．已知p是r的充分不必要条件，s是r的必要条件，q是s的必要条件，那么p是q成立的 条件。（填“充分不必要”“必要不充分”、“充要”或“既不充分也不必要” ） 13．若方程  所表示的曲线为C，给出下列四个命题：①若C为椭圆，则1<t<4; ②若C为双曲线，则t>4或t<1； ③曲线C不可能是圆； ④若C表是椭圆，且长轴在x轴上，则  .其中真命题的序号为 （把所有正确命题的序号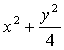都填在横线上） 14．函数y=  的单调增区间是 ，减区间是 . 15．求与椭圆  有共同焦点，且过点 的双曲线方程，并且求出这条双曲线的实轴长、焦距、离心率。16．设椭圆方程为  =1，过点M（0，1）的直线l交椭圆于点A、B，O为坐标原点，点P满足 ，当l绕点M旋转时，求动点P的轨迹方程.17．设f(x)=x3-  x2-2x+5（1）求函数f(x)的单调区间。（2）求极值点与极值。 18．已知椭圆 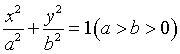 的离心率 ，过点 和 的直线与原点的距离为 。⑴求椭圆的方程； ⑵已知定点  ，若直线 与椭圆交于 两点，问：是否存在 的值，使以 为直径的圆过 点？请说明理由。参考答案： 1.B; 2.C; 3.D; 4.A; 5.C; 6.B; 7.C; 8.A; 9.C; 10.A; 11.  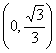; 12. 充分不必要; 13. （2）;14.   ;15.  16(1)在   上为单调递增区间,在 上为单调递减区间.(2)x=1时,y=  ,x= 时,y= 17．解：设P（x，y）是所求轨迹上的任一点， ①当斜率存在时，直线l的方程为y=kx+1，A（x1，y1），B（x2，y2）， 由  得：（4+k2）x2+2kx－3=0， x1+x2=－ y1+y2= ，由  得：（x，y）= （x1+x2，y1+y2），即：  消去k得：4x2+y2－y=0 当斜率不存在时，AB的中点为坐标原点，也适合方程所以动点P的轨迹方程为：4x2+y2－y= 0。 18.  (责任编辑：admin) |
- 上一篇：没有了
- 下一篇：2.5圆锥曲线单元测试