2.5圆锥曲线单元测试
http://www.newdu.com 2025/11/27 12:11:04 人民教育出版社 佚名 参加讨论
2.5圆锥曲线单元测试 1)如果实数 A、 2)若直线 A、 3)已知椭圆 (A)10 (B)20 (C)2 4)椭圆 (A)15 (B)12 (C)10 (D)8 5)椭圆 (A)9 (B)12 (C)10 (D)8 6)椭圆 (A)3(B) 7)以坐标轴为对称轴、渐近线互相垂直、两准线间距离为2的双曲线方程是( ) (A) (C) 8)双曲线 (A)6 (B)8 (C)10 (D)12 9)过双曲线 (A)28 (B) 10)双曲线虚轴上的一个端点为M,两个焦点为F1、F2, (A) 11)过抛物线 (A)2a (B) 12) 如果椭圆 (A) 13)与椭圆 14)离心率 15)过抛物线 16)若直线l过抛物线 18) 已知双曲线与椭圆 19) 抛物线 20)求两条渐近线为 21)已知直线y=ax+1与双曲线3x2-y2=1交于A、B两点,(1)若以AB线段为直径的圆过坐标原点,求实数a的值。(2)是否存在这样的实数a,使A、B两点关于直线 参考答案: 1.D; 2.D; 3.D; 4.B; 5.A; 6.D; 7.D; 8.B; 9.C; 10.B; 11. C; 12.D; 13. 17. 解:由已知条件得椭圆的焦点在x轴上,其中c= 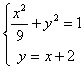 ,消去y得, ,消去y得, 设A( 所以 也就是说线段AB中点坐标为(- 18. 解:由于椭圆焦点为F(0, 从而c=4,a=2,b=2 所以求双曲线方程为: 19. 解:由于 = (1)a (2)a>时, 当且仅当x=a-1时, 所以 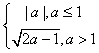 . .20. 解:设双曲线方程为x2-4y2= 联立方程组得:  ,消去y得,3x2-24x+(36+ ,消去y得,3x2-24x+(36+设直线被双曲线截得的弦为AB,且A( 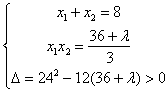 那么:|AB|= 解得: 21. 解:(1)联立方程 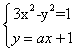 ,消去y得:(3-a2)x2-2ax-2=0. ,消去y得:(3-a2)x2-2ax-2=0.设A( 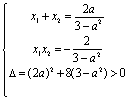 由于以AB线段为直径的圆经过原点,那么: 所以: (2)假定存在这样的a,使A( 那么: 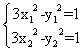 ,两式相减得: ,两式相减得:因为A( 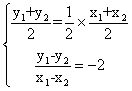 代入(*)式得到:-2=6,矛盾。 也就是说:不存在这样的a,使A( (责任编辑:admin) |
- 上一篇:选修1-1综合测试
- 下一篇:3.5导数及其运用单元测试