第四章《圆与方程》复习测试题(二)
三、解答题
11.已知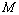 为圆 为圆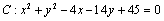 上任意一点,点 上任意一点,点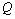 的坐标为(-2,3). 的坐标为(-2,3).
⑴求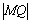 的最大值和最小值; 的最大值和最小值;
⑵若P(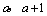 )在圆 )在圆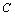 上,求线段 上,求线段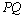 的长及直线 的长及直线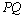 的斜率. 的斜率.
考查目的:考查圆的方程的互化,直线的斜率,点和圆、直线和圆的位置关系及其运用.
答案:⑴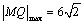 , , ;⑵ ;⑵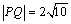 , ,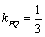 . .
解析:⑴圆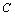 的方程可化为 的方程可化为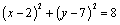 ,∴圆心 ,∴圆心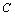 的坐标为(2,7),半径 的坐标为(2,7),半径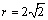 ,∴ ,∴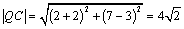 ,∴ ,∴ , ,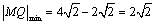 . .
⑵∵点P(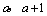 )在圆 )在圆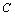 上,∴ 上,∴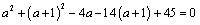 ,解得 ,解得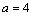 ,∴点P的坐标为(4,5),∴ ,∴点P的坐标为(4,5),∴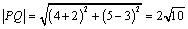 , ,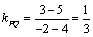 . .
12.设圆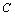 上的点A(2,3)关于直线 上的点A(2,3)关于直线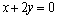 的对称点仍在圆 的对称点仍在圆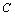 上,且圆 上,且圆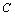 与直线 与直线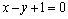 相交的弦长为 相交的弦长为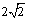 ,求圆 ,求圆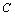 的方程. 的方程.
考查目的:考查圆的方程及其性质,直线与圆的位置关系.
答案:圆的方程为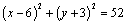 或 或 . .
解析:设圆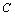 的方程为 的方程为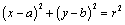 .∵圆 .∵圆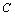 上的点A(2,3)关于直线 上的点A(2,3)关于直线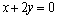 的对称点仍在圆 的对称点仍在圆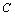 上,∴圆心 上,∴圆心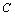 在 在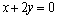 上,∴ 上,∴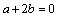 ①. ①.
∵圆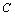 被直线 被直线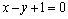 截得的弦长为 截得的弦长为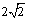 ,∴ ,∴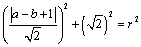 ②. ②.
由点A(2,3)在圆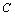 上,得 上,得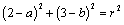 ③. ③.
联立①②③,解得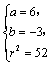 或 或
∴圆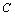 的方程为 的方程为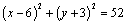 或 或 . .
13.已知圆C: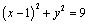 内有一点P(2,2),过点P作直线 内有一点P(2,2),过点P作直线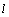 交圆C于A、B两点. 交圆C于A、B两点.
⑴当直线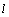 经过圆心C时,求直线 经过圆心C时,求直线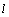 的方程; 的方程;
⑵当弦AB被点P平分时,写出直线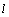 的方程; 的方程;
⑶当直线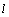 的倾斜角为 的倾斜角为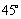 时,求弦AB的长. 时,求弦AB的长.
考查目的:考查直线与圆的位置关系,以及直线方程的求法.
答案:⑴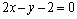 ;⑵ ;⑵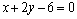 ;⑶ ;⑶ . .
解析:⑴已知圆C: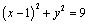 的圆心为C(1,0).∵直线 的圆心为C(1,0).∵直线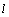 经过点P、C,∴直线 经过点P、C,∴直线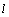 的斜率为2,直线 的斜率为2,直线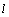 的方程为 的方程为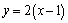 ,即 ,即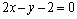 . .
⑵当弦AB被点P平分时,直线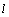 ⊥PC,∴直线 ⊥PC,∴直线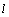 的方程为 的方程为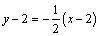 ,即 ,即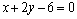 . .
⑶当直线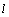 的倾斜角为 的倾斜角为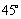 时,斜率为1,直线 时,斜率为1,直线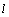 的方程为 的方程为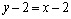 ,即 ,即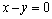 .又∵圆心C(1,0)到直线 .又∵圆心C(1,0)到直线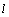 : :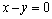 的距离为 的距离为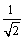 ,圆C的半径为3,∴弦AB的长为 ,圆C的半径为3,∴弦AB的长为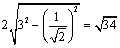 . .
14.已知圆P: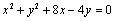 与以原点为圆心的圆Q关于直线 与以原点为圆心的圆Q关于直线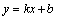 对称. 对称.
⑴求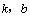 的值; 的值;
⑵若两圆的交点为A、B,求∠AOB的度数.
考查目的:考查直线和圆的位置关系,圆和圆的位置关系及其综合应用.
答案:⑴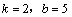 ;⑵ ;⑵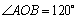 . .
解析:⑴圆P: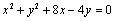 的方程可写成 的方程可写成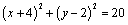 . .
∵圆P: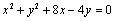 和以原点为圆心的圆Q关于直线 和以原点为圆心的圆Q关于直线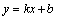 对称, 对称,
∴直线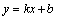 是以两圆圆心P、Q为端点的线段的垂直平分线, 是以两圆圆心P、Q为端点的线段的垂直平分线,
∴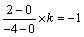 ,解得 ,解得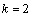 . .
∵点(0,0)与(-4,2)的中点(-2,1)在直线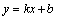 上,∴ 上,∴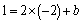 ,解得 ,解得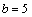 . .
⑵圆心P(-4,2)到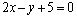 的距离为 的距离为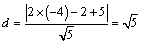 , ,
又∵圆P的半径为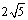 ,∴ ,∴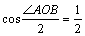 ,由 ,由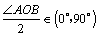 得 得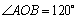 . .
15.(2008江苏)设平面直角坐标系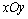 中,设二次函数 中,设二次函数 的图像与两坐标轴有三个交点,经过这三个交点的圆记为C.求: 的图像与两坐标轴有三个交点,经过这三个交点的圆记为C.求:
⑴求实数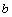 的取值范围; 的取值范围;
⑵求圆C的方程;
⑶问圆C是否经过某定点(其坐标与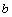 无关)?请证明你的结论. 无关)?请证明你的结论.
考查目的:考查二次函数图像和性质、圆的方程的求法.
答案:⑴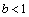 且 且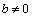 ;⑵ ;⑵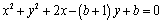 ;⑶圆C必过定点(0,1),(-2,1). ;⑶圆C必过定点(0,1),(-2,1).
解析:⑴∵圆C经过二次函数 图象与坐标轴的三个交点,∴ 图象与坐标轴的三个交点,∴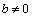 .令 .令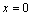 ,得抛物线与 ,得抛物线与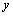 轴的交点是(0, 轴的交点是(0,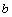 ).令 ).令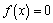 ,得 ,得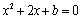 ,此时 ,此时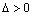 ,解得 ,解得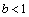 .∴实数 .∴实数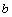 的取值范围是 的取值范围是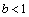 且 且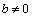 . .
⑵设所求圆的一般方程为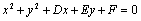 .令 .令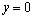 ,得 ,得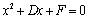 ,这与 ,这与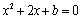 是同一个方程,∴ 是同一个方程,∴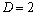 , ,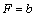 .令 .令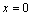 ,得 ,得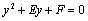 ,此方程有一个根为 ,此方程有一个根为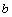 ,代入得 ,代入得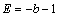 .∴圆C的方程为 .∴圆C的方程为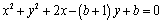 . .
⑶圆C过定点,证明如下:假设圆C经过定点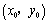 .将该点坐标 .将该点坐标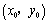 代入圆C的方程,并变形得 代入圆C的方程,并变形得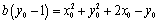 ①.①式对所有满足 ①.①式对所有满足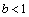 且 且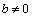 的实数 的实数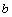 都成立,必须 都成立,必须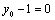 且 且 ,解得 ,解得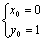 或 或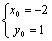 .经检验知,点(0,1),(-2,1)均在圆C上,∴圆C经过定点. .经检验知,点(0,1),(-2,1)均在圆C上,∴圆C经过定点.
(责任编辑:admin)
|
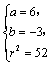 或
或