《4.3 空间直角坐标系》测试题
一、选择题
1.在空间直角坐标系中,已知点P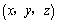 给出下列4条叙述: 给出下列4条叙述:
①点P关于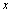 轴的对称点的坐标是 轴的对称点的坐标是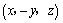 ; ;
②点P关于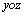 平面的对称点的坐标是 平面的对称点的坐标是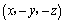 ; ;
③点P关于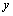 轴的对称点的坐标是 轴的对称点的坐标是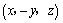 ; ;
④点P关于原点的对称点的坐标是 . .
其中正确的个数是( ).
A.3 B.2 C.1 D.0
考查目的:考查空间直角坐标系中对称点的坐标特征.
答案:C.
解析:根据空间直角坐标系中,关于线和面对称的点的坐标的特征可以判断,点P关于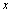 轴的对称点的坐标是 轴的对称点的坐标是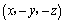 ,关于 ,关于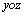 平面的对称点的坐标是 平面的对称点的坐标是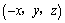 ,关于 ,关于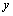 轴的对称点的坐标是 轴的对称点的坐标是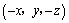 ,关于原点的对称点的坐标是 ,关于原点的对称点的坐标是 .答案应选C. .答案应选C.
2.已知空间直角坐标系中点P(1,2,3),现在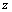 轴上取一点Q,使得 轴上取一点Q,使得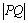 最小,则Q点的坐标为( ). 最小,则Q点的坐标为( ).
A.(0,0,1) B.(0,0,2) C.(0,0,3) D.(0,1,0)
考查目的:考查空间两点间的距离公式的应用.
答案:C.
解析:设点Q的坐标为(0,0,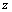 ),则 ),则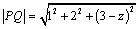 ,当 ,当 时, 时,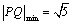 . .
3.以正方体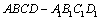 的棱AB、AD、 的棱AB、AD、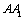 所在的直线分别为 所在的直线分别为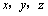 轴建立空间直角坐标系,若正方体的棱长为1,则棱 轴建立空间直角坐标系,若正方体的棱长为1,则棱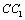 中点的坐标为( ). 中点的坐标为( ).
A.(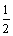 ,1,1) B.(1, ,1,1) B.(1,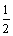 ,1) C.(1,1, ,1) C.(1,1,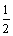 ) D.( ) D.(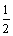 , ,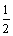 ,1) ,1)
考查目的:考查空间直角坐标系中的中点坐标公式.
答案:C.
解析:分别以正方体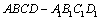 的棱AB、AD、 的棱AB、AD、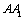 所在的直线为 所在的直线为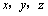 轴建立空间直角坐标系,依题意得,点 轴建立空间直角坐标系,依题意得,点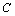 的坐标为(1,1,0),点 的坐标为(1,1,0),点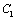 的坐标(1,1,1),所以 的坐标(1,1,1),所以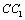 中点的坐标为(1,1, 中点的坐标为(1,1,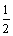 ). ).
二、填空题
4.(2009安徽)在空间直角坐标系中,已知点A(1,0,2),B(1,-3,1),点M在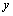 轴上,且点M到点A与到点B的距离相等,则M的坐标是 . 轴上,且点M到点A与到点B的距离相等,则M的坐标是 .
考查目的:考查空间直角坐标系中两点间的距离公式的应用.
答案:(0,-1,0).
解析:设点M的坐标为(0,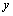 ,0),则 ,0),则 ,解得 ,解得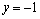 ,∴点M的坐标为(0,-1,0). ,∴点M的坐标为(0,-1,0).
5.设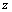 为任意实数,则点P(1,2, 为任意实数,则点P(1,2,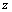 )的集合对应的图形为 . )的集合对应的图形为 .
考查目的:考查对空间点的坐标和点集所对应的图形的认识.
答案:过点(1,2,0)且平行于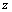 轴的一条直线. 轴的一条直线.
解析:因为点P(1,2,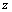 )在空间直角坐标系中,横坐标、纵坐标不变,只有竖坐标是任意实数,所以点P(1,2, )在空间直角坐标系中,横坐标、纵坐标不变,只有竖坐标是任意实数,所以点P(1,2,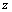 )表示的点集是经过点(1,2,0)且平行于 )表示的点集是经过点(1,2,0)且平行于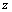 轴(或与平面 轴(或与平面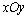 垂直)的一条直线. 垂直)的一条直线.
6.若P在坐标平面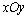 内,点A的坐标为(0,0,4),且 内,点A的坐标为(0,0,4),且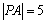 ,则点P的轨迹是__________. ,则点P的轨迹是__________.
考查目的:考查空间直角坐标系中动点的轨迹的求法.
答案:坐标平面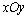 内以(0,0,0)为圆心,以3为半径的圆. 内以(0,0,0)为圆心,以3为半径的圆.
解析:设点P的坐标为P(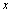 , ,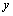 ,0),依题意得 ,0),依题意得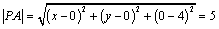 ,整理得 ,整理得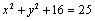 ,∴ ,∴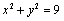 ,这个方程表示,P点的轨迹是坐标平面 ,这个方程表示,P点的轨迹是坐标平面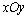 内以点(0,0,0)为圆心,以3为半径的圆. 内以点(0,0,0)为圆心,以3为半径的圆.
三、解答题
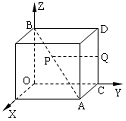
7.以棱长为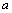 的正方体的三条棱为坐标轴,建立空间直角坐标系 的正方体的三条棱为坐标轴,建立空间直角坐标系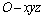 ,点P在正方体的对角线AB上,点Q在正方体的棱CD上.若点P为对角线AB的中点,且点Q在棱CD上运动,求PQ的最小值. ,点P在正方体的对角线AB上,点Q在正方体的棱CD上.若点P为对角线AB的中点,且点Q在棱CD上运动,求PQ的最小值.
考查目的:考查空间直角坐标系,空间两点间的距离公式与二次函数的最值.
答案: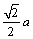 . .
解析:由题意得A(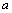 , ,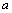 ,0),B(0,0, ,0),B(0,0,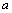 ),C(0, ),C(0,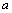 ,0),D(0, ,0),D(0,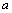 , ,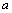 ).∵点P为对角线AB的中点,∴点P的坐标为( ).∵点P为对角线AB的中点,∴点P的坐标为(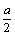 , ,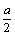 , ,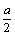 ).设点Q的坐标为(0, ).设点Q的坐标为(0,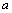 , ,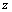 ),则 ),则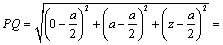
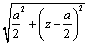 ,∴当 ,∴当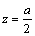 时,PQ取得最小值 时,PQ取得最小值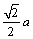 ,此时Q为CD的中点. ,此时Q为CD的中点.
8.在空间直角坐标系中,已知A(3,0,1)和B(1,0,-3),试问:
⑴在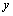 轴上是否存在点 轴上是否存在点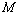 ,满足 ,满足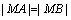 ? ?
⑵在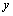 轴上是否存在点 轴上是否存在点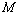 ,使 ,使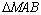 为等边三角形?若存在,试求出点 为等边三角形?若存在,试求出点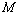 坐标. 坐标.
考查目的:考查空间两点间的距离公式的应用.
答案:⑴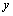 轴上任意一点都满足条件;⑵在 轴上任意一点都满足条件;⑵在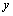 轴上存在点 轴上存在点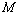 ,使得 ,使得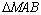 为等边三角形,点 为等边三角形,点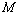 的坐标为(0, 的坐标为(0,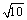 ,0),或(0, ,0),或(0,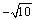 ,0). ,0).
解析:⑴假设在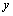 轴上存在点 轴上存在点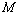 ,使得 ,使得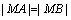 .∵ .∵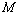 在 在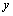 轴上,∴可设点M的坐标为(0, 轴上,∴可设点M的坐标为(0,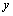 ,0).由 ,0).由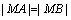 得 得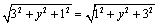 ,显然,此式对任意的 ,显然,此式对任意的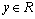 恒成立,说明 恒成立,说明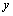 轴上所有的点都满足关系 轴上所有的点都满足关系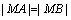 ; ;
⑵假设在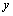 轴上存在点 轴上存在点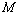 ,使 ,使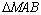 为等边三角形.由⑴知, 为等边三角形.由⑴知,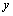 轴上任意一点都有 轴上任意一点都有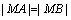 ,∴只要 ,∴只要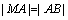 就可以使得 就可以使得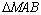 是等边三角形.∵ 是等边三角形.∵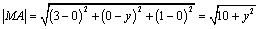 , ,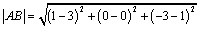 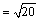 ,∴ ,∴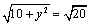 ,解得 ,解得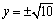 ,∴在 ,∴在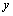 轴上存在点 轴上存在点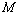 ,使得 ,使得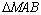 为等边三角形,符合题意的点 为等边三角形,符合题意的点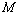 的坐标为(0, 的坐标为(0,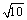 ,0),或(0, ,0),或(0,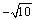 ,0). ,0).
(责任编辑:admin)
|
