第二章《点、直线、平面之间的位置关系》测试题(一)
一、选择题
1.(2010全国1文)在直三棱柱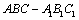 (侧面都是矩形的棱柱)中,若 (侧面都是矩形的棱柱)中,若 , ,
 ,则异面直线 ,则异面直线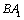 与 与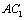 所成的角等于( ). 所成的角等于( ).
A.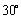 B. B.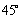 C. C.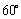 D. D.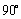
考查目的:考查直三棱柱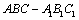 的性质,异面直线所成的角的求法. 的性质,异面直线所成的角的求法.
答案:C.
解析:延长CA到D,使得 ,则 ,则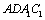 为平行四边形, 为平行四边形, 就是异面直线 就是异面直线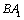 与 与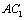 所成的角,又∵三角形 所成的角,又∵三角形 为等边三角形,∴ 为等边三角形,∴ . .
2.在空间中,下列命题正确的是( ).
A.若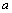 ∥ ∥ , , ∥ ∥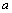 ,则 ,则 ∥ ∥ B.若 B.若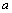 ∥ ∥ , , ∥ ∥ , ,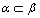 , ,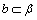 ,则 ,则 ∥ ∥
C.若 ∥ ∥ , , ∥ ∥ ,则 ,则 ∥ ∥ D.若 D.若 ∥ ∥ , ,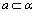 ,则 ,则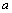 ∥ ∥
考查目的:考查直线与平面、平面与平面平行的判定.
答案:D.
解析:若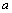 ∥ ∥ , , ∥ ∥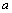 ,则 ,则 ∥ ∥ 或 或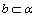 ,故A错误;由平面与平面平行的判定定理知,B错误;若 ,故A错误;由平面与平面平行的判定定理知,B错误;若 ∥ ∥ , , ∥ ∥ ,则 ,则 ∥ ∥ 或 或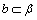 ,故C错误. ,故C错误.
3.设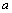 , , , ,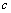 表示三条不同的直线, 表示三条不同的直线, , , 表示两个不同的平面,则下列命题不正确的是( ). 表示两个不同的平面,则下列命题不正确的是( ).
A.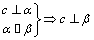 B. B.
C.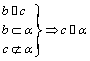 D. D.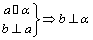
考查目的:考查直线与平面平行、垂直的转化.
答案:D.
解析:由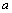 ∥ ∥ , , ⊥ ⊥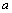 可得, 可得, 与 与 的位置关系有: 的位置关系有: ∥ ∥ , ,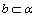 , , 与 与 相交,∴D不正确. 相交,∴D不正确.
4.(2010宁夏海南)如图,正方体 的棱长为1,线段 的棱长为1,线段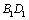 上有两个动点E,F,且 上有两个动点E,F,且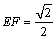 ,则下列结论中错误的是( ). ,则下列结论中错误的是( ).

A.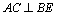 B.三棱锥 B.三棱锥 的体积为定值 的体积为定值
C. D.异面直线 D.异面直线 所成的角为定值 所成的角为定值
考查目的:考查空间直线、平面之间平行和垂直关系综合应用的能力.
答案:D.
解析:A正确,易证 ,从而 ,从而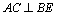 ;B正确,可用等积法求得;C显然正确,∵ ;B正确,可用等积法求得;C显然正确,∵ ,∴ ,∴ ;D错误. ;D错误.
5.(2012重庆理)设四面体的六条棱的长分别为1,1,1,1, 和 和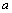 ,且长为 ,且长为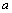 的棱与长为 的棱与长为 的棱异面,则 的棱异面,则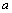 的取值范围是( ). 的取值范围是( ).
A. B. B. C. C.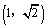 D. D.
考查目的:考查空间直线与直线之间的位置关系,以及有关计算的能力.
答案:A.
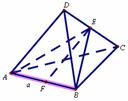
解析:如图所示的四面体 ,设 ,设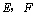 为 为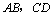 中点,在 中点,在 中, 中,
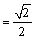 ,则 ,则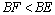 , , . .
6.如图,平面 ⊥平面 ⊥平面 ,A∈ ,A∈ ,B∈ ,B∈ ,AB与两平面 ,AB与两平面 , , 所成的角分别为 所成的角分别为 和 和 ,过A、B分别作两平面交线的垂线,垂足为 ,过A、B分别作两平面交线的垂线,垂足为 、 、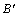 ,则 ,则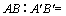 ( ). ( ).

A.2∶1 B.3∶1 C.3∶2 D.4∶3
考查目的:考查直线与平面所成的角,以及二面角概念的综合运用.
答案:A.
解析:在平面 内,过 内,过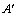 作 作 , , 且 且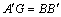 ,连结 ,连结 和 和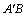 ,因为平面 ,因为平面 ⊥平面 ⊥平面 ,所以 ,所以 和 和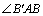 即为 即为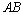 和平面 和平面 和平面 和平面 所成的角,先解 所成的角,先解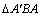 和 和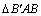 求线段 求线段 和 和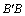 的长,再解 的长,再解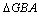 . .
二、填空题
7.如图,已知PA⊥平面ABC,BC⊥AC,则图中直角三角形的个数为________.

考查目的:考查直线与直线、直线与平面垂直关系的判定.
答案:4.
解析:由直线与平面垂直关系可知,图中直角三角形共有4个.
8.(2007湖北理)平面 外有两条直线 外有两条直线 和 和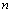 ,如果 ,如果 和 和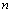 在平面 在平面 内的射影分别是 内的射影分别是 和 和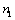 ,给出下列四个命题: ,给出下列四个命题:
① ⊥ ⊥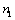 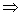  ⊥ ⊥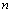 ;② ;② ⊥ ⊥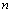 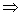  ⊥ ⊥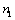 ;③ ;③ 与 与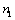 相交 相交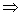  与 与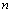 相交或重合;④ 相交或重合;④ 与 与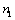 平行 平行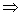  与 与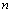 平行或重合. 平行或重合.
其中不正确的命题是 .
考查目的:考查空间两条直线的位置关系.
答案:①②③④.
解析:①如图 ⊥ ⊥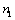 ,但 ,但 与 与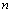 不垂直;② 不垂直;② ⊥ ⊥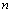 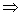  ⊥ ⊥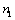 或 或 与 与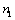 重合;③ 重合;③ 与 与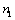 相交 相交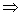  与 与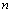 相交或重合或异面;④ 相交或重合或异面;④ 与 与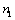 平行 平行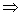  与 与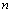 平行或异面,所以四个命题均不正确. 平行或异面,所以四个命题均不正确.

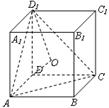
9.(2010全国1文)在正方体 中, 中, 与平面 与平面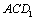 所成角的余弦值为________. 所成角的余弦值为________.
考查目的:考查正方体的性质、直线与平面所成的角的求法.
答案: . .
解析:∵ ∥ ∥ ,∴ ,∴ 与平面 与平面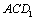 所成的角和 所成的角和 与平面 与平面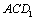 所成的角相等.设DO⊥平面 所成的角相等.设DO⊥平面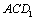 ,由等体积法得 ,由等体积法得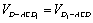 ,即 ,即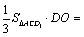
 .设 .设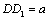 ,则 ,则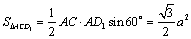 , , , ,
∴ ,记 ,记 与平面 与平面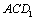 所成角为 所成角为 ,则 ,则 ,∴ ,∴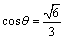 . .
10.(2009浙江理)如图,在长方形 中, 中, , , , ,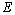 为 为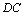 的中点, 的中点, 为线段 为线段 (端点除外)上一动点.现将 (端点除外)上一动点.现将 沿 沿 折起,使平面 折起,使平面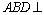 平面 平面 .在平面 .在平面 内过点 内过点 作 作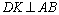 , ,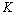 为垂足.设 为垂足.设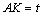 ,则 ,则 的取值范围是 . 的取值范围是 .

考查目的:考查直线与平面的位置关系,以及二面角概念的综合应用.
答案: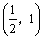 . .
解析:当F位于DC的中点时,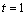 ;随着点F移动到与点C重合时,∵ ;随着点F移动到与点C重合时,∵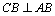 , , ,∴ ,∴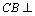 平面 平面 ,∴ ,∴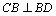 .对于 .对于 , , ,∴ ,∴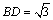 .又∵ .又∵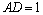 , , ,∴ ,∴ ,∴ ,∴ ,因此 ,因此 的取值范围是 的取值范围是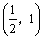
(责任编辑:admin)
|