高中学习网-人民教育出版社人教版部编同步解析与测评答案-电子课本资料下载-知识点学习方法与技巧补课解题技巧学习计划表总结-人教网-高中试卷网题库网-中学学科网

首页 > 高中数学A版 > 必修二 > 同步检测 >

1.3柱、锥、台、球的表面积和体积

http://www.newdu.com 2025/05/25 10:05:20 人民教育出版社 佚名 参加讨论


    1.3柱、锥、台、球的表面积和体积
    考纲要求：了解柱、锥、台、球的表面积和体积的计算公式（不要求记忆公式）；会求一些简单几何体的表面积和体积，体会积分思想在计算表面积和体积的运用．
    重难点：了解柱、锥、台、球的表面积和体积的计算公式，会求一些简单几何体的表面积和体积，体会积分思想在计算表面积和体积的运用．
    经典例题：在三棱柱ABC—DEF中，已知AD到面BCFE的距离为h，平行四边形BCFE的面积为S．
    求：三棱柱的体积V．
    当堂练习：
    1．长方体ABCD-A1B1C1D1的AB=3，AD=2，CC1=1，一条绳子从A沿着表面拉到点C1，绳子的最短长度是（　　）
     A．+1         B．           C．         D．
    2．若球的半径为R，则这个球的内接正方体的全面积等于（　　）
    A．8R2             B． 9R2            C．10R2            D．12R2
    3．边长为5cm的正方形EFGH是圆柱的轴截面, 则从E点沿圆柱的侧面到相对顶点G的最短距离是（　　）
     A． 10cm            B． 5cm         C． 5cm    D．cm
    4．球的大圆面积扩大为原大圆面积的4倍，则球的表面积扩大成原球面积的（     ）
     A．2倍             B． 4倍            C． 8倍           D．16倍
    5．三个球的半径之比为1：2：3，那么最大球的表面积是其余两个球的表面积之和的（     ）
     A．1倍             B．2倍             C．1倍         D．1倍
    6．正方体的全面积是a2,它的顶点都在球面上，这个球的表面积是（     ）
     A．            B．            C．         D．
    7．两个球的表面积之差为48,它们的大圆周长之和为12,这两个球的半径之差为（     ）
    A．4              B． 3               C． 2            D． 1
    8．已知正方体的棱长为a，过有公共顶点的三条棱的中点的截面分别截去8个角，则剩余部分的体积是（     ）
    A．a3               B．a3               C．a3            D．a3
    9.正方形ABCD的边长为1，E、F分别为BC、CD的中点，沿AE，EF，AF折成一个三棱锥，使B，C，D三点重合，那么这个三棱锥的体积为（     ）
     A．                B．            C．           D．
    10.棱锥V-ABC的中截面是A1B1C1，则三棱锥V-A1B1C1与三棱锥A-A1BC的体积之比是（    ）
    A．1：2              B． 1：4             C．1：6           D．1：8
    11. 两个球的表面积之比是1：16，这两个球的体积之比为（     ）
    A．1：32              B．1：24             C．1：64          D． 1：256
    12．两个球的体积之比为8：27，那么，这两个球的表面积之比为（     ）
     A．2：3                 B．4：9             C．        D．
    13．棱长为a的正方体内有一个球，与这个正方体的12条棱都相切，则这个球的体积应为（     ）
    A． 43      　　　　　B．       　　C．       　D．
    14．半径为R的球的外切圆柱的表面积是______________．
    15．E是边长为2的正方形ABCD边AD的中点，将图形沿EB、EC折成三棱锥A-BCE（A，D重合）， 则此三棱锥的体积为____________．
    16.直三棱柱的体积是V，D、E分别在、上，线段DE经过矩形的中心，则四棱锥C-ABED的体积是________________．
    17．一个直角三角形的两条直角边的长分别为3cm和4cm, 将这个直角三角形以斜边为轴旋转一周,所得旋转体的体积是________________．
    18．圆锥的底面半径为5cm, 高为12cm, 当它的内接圆柱的底面半径为何值时, 圆锥的内接圆柱的全面积有最大值?最大值是多少?
    19．A、B、C是球面上三点，已知弦AB=18cm，BC=24cm，AC=30cm，平面ABC与球心O的距离恰好为球半径的一半，求球的面积．
    
    20．圆锥轴截面为顶角等于1200的等腰三角形, 且过顶点的最大截面面积为8, 求这圆锥的全面积S和体积V．
    21．已知ABCD-A1B1C1D1是棱长为a的正方体， E、F分别为棱AA1与CC1的中点，求四棱锥A1-EBFD1的体积．
    参考答案：
    经典例题： 解法一：把三棱柱补成一平行六面体EFDG—BCAH，可看成以s为底，以h为高，则体积为sh． VABC-DEF= 这就是用补的方法求体积．
    解法二：连DB、DC、BF，把三棱柱分割成三个等体积的三棱锥，如D—BEF就是以s为底，高为h的三棱锥，则VD-BEF=   则VABC-DEF=3 VD-BEF=．
    当堂练习：
    1.C; 2.A; 3.D; 4.B; 5.C; 6.B; 7.C; 8.C; 9.B; 10.B; 11.C; 12.B; 13.C; 14. 6R2; 15. ; 16. ;  17. ;
    18. 如图 ,SAB是圆锥的轴截面, 其中SO=12, OB=5.设圆锥内接圆柱底面半径为O1C=x , 由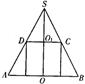与相似, 则
        OO1=SO-SO1=12-,则圆柱的全面积S=S侧+2S底=2则当时,S取到最大值．
    
    19. 解：AB2+BC2=AC2， ABC为直角三角形，  ABC的外接圆O1的半径r=15cm，
    因圆O1即为平面ABC截球O所得的圆面，因此有R2=（）2+152，
    R2=300，S球=4R2=1200（cm2）.
    20. 解:设母线长为, 当截面的两条母线互相垂直时, 有最大的截面面积. 此时,
    底面半径,高则S全=
    21. 解：四棱锥A1-EBFD1的底面是菱形，连接EF，则，平面ABB1A1，
       三棱锥F-EBA1的高是CC1到平面AB1的距离，即棱长a，   S        
    
     (责任编辑：admin)



    最近关注
    热点内容