第二章《点、直线、平面之间的位置关系》测试题(二)
http://www.newdu.com 2025/05/26 01:05:35 人民教育出版社 佚名 参加讨论
第二章《点、直线、平面之间的位置关系》测试题(二) 三、解答题 11.(2012上海理改编)如图,在四棱锥 ⑴四棱锥 ⑵异面直线 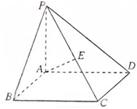 考查目的:考查异面直线所成角的概念及其求法. 答案:⑴ 解析:⑴根据题意四棱锥 12.(2011湖南文)如图,在圆锥PO中,已知  ⑴证明:AC ⑵求直线OC和平面PAC所成角的正弦值. 考查目的:考查直线与平面垂直的判定,直线与平面所成角的计算,以及空间想象能力. 答案:⑴略,⑵ 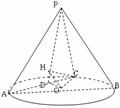 解析:⑴∵OA=OC,D是AC的中点,∴AC⊥OD.又∵PO⊥底面⊙O, ⑵由⑴知,AC⊥平面POD.又∵ 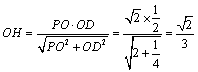 ;在 ;在13.(2010陕西文)如图,在四棱锥P—ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AP=AB,BP=BC=2,E,F分别是PB,PC的中点. ⑴证明:EF∥平面PAD; ⑵求三棱锥E—ABC的体积V. 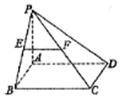 考查目的:考查直线与平面平行的判定,以及三棱锥的体积计算. 答案:⑴略;⑵ 解析:⑴在△PBC中,E,F分别是PB,PC的中点,∴EF∥BC.又∵BC∥AD,∴EF∥AD,∵AD ⑵连接AE,AC,EC,过E作EG∥PA交AB于点G,则BG⊥平面ABCD,且 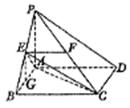 14.(2010四川理)已知正方体 ⑴求证:OM为异面直线 ⑵求二面角 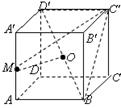 考查目的:考查异面直线、直线与平面垂直、二面角、正方体等基础知识,空间想象能力和逻辑推理能力. 答案:⑴略;⑵ 解析:⑴连结AC,取AC中点K,则K为BD的中点,连结OK.∵M是棱 由 ∴OM为异面直线 ⑵取 ∴二面角 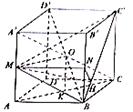 15.(2012湖南理)如图,在四棱锥 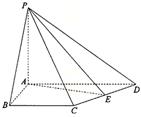 ⑴证明:CD⊥平面PAE; ⑵若直线 考查目的:考查直线与平面垂直的判定,直线和平面所成角的运用,体积计算以及综合运用立体几何知识解决问题的能力. 答案:⑴略;⑵ 解析:⑴连接 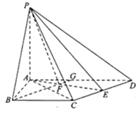 ⑵过点 (责任编辑:admin) |
- 上一篇:2.1.2 直线的方程
- 下一篇:2.3空间直角坐标系