|
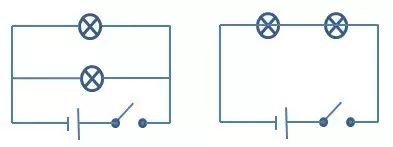
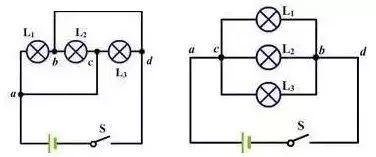
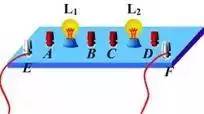
一、串联与并联——定义 ◆ 串联电路: 将电路元器件首尾依次连接起来便形成了串联电路。串联电路只有一条通路,各个电路元器件之间相互影响,只要有一处非正常工作,则该电路就没有导通,为断路,用电器无法正常工作。例如装饰用的“满天星”小彩灯便是串联电路在日常生活中的应用。 ◆ 并联电路: 将电路元器件并列连接在电路的两点间便组成了并联电路。并联电路有多条通路,各个支路间电路元器件不互相影响,可以独立工作,当某一支路无法正常工作时,其他支路仍可以正常工作,不受其影响。例如家庭中的电灯、电风扇、电冰箱、电视机等用电器都是并联在电路中的。 二、串联与并联——特点 ◆ 串联电路: 1. 由于恒定电流电路中各处电荷是稳定的,因此,单位时间内通过串联电路各部分的电荷量相等,也就是串联电路电流处处相等,即I总=I1=I2=……=In; 2. 串联电路总电压等于各用电器电压之和,即U总=U1+U2+U3+……+Un; 3. 由电流处处相等、总电压为各用电器电压之和、电阻R=U/I得:串联电路等效电阻等于各电阻之和,即R总=R1+R2+R3+……+Rn; 4. 由电流处处相等、总电压为各用电器电压之和、功率P=UI得:串联电路总功率等于各功率之和,即P总=P1+P2+P3+……+Pn。 ◆ 并联电路: 1. 并联电路干路电流等于各支路电流之和,即I总=I1+I2+……+In; 2. 并联电路中各并联元器件两端电压相等,即U总=U1=U2=U3=……=Un; 3. 由各元器件两端电压相等、干路电流等于各支路电流之和、电阻R=U/I得:并联电路等效电阻的倒数等于各电阻的倒数和,即1/R总=1/R1+1/R2+1/R3+……+1/Rn; 4. 由各元器件两端电压相等、干路电流等于各支路电流之和、功率P=UI得:并联电路总功率等于各功率之和,即R总=P1+P2+P3+……+Pn。 三、串联和并联——区别 1. 串联电路只有一条路径,并联电路有多条路径; 2. 串联电路各用电器之间相互影响,并联电路各用电器之间可以独立工作; 3. 串联电路中一个开关可以控制所有用电器,并联电路需在干路支路上放置多个开关才可以实现对整个电路的控制; 4. 串联电路中有I总=I1=I2=……=In,并联电路中有I总=I1+I2+……+In; 5. 串联电路中有U总=U1+U2+U3+……+Un,并联电路中有U总=U1=U2=U3=……=Un; 6. 串联电路中有R总=R1+R2+R3+……+Rn,并联电路中有1/R总=1/R1+1/R2+1/R3+……+1/Rn。 四、识别串联和并联的方法 ◆ 定义法 若电路中的各元件是逐个顺次连接起来的,则电路为串联电路,若各元件“首首相接,尾尾相连”并列地连在电路两点之间,则电路就是并联电路。 ◆ 电流流向法 从电源的正极(或负极)出发,沿电流流向,分析电流通过的路径。若电流在某处分支,又在另一处汇合,则分支处到汇合处之间的电路是并联的(如左图所示);若只有一条路径通过所有的用电器,则这个电路是串联的(如右图所示)。 ◆ 节点法 就是在识别电路的过程中,不论导线有多长,只要其间没有电源、用电器等,导线两端点均可以看成同一个点,从而找出各用电器两端的公共点。 具体方法:先在图中各节点处用字母表示出来,如左图所示。 由“节点法”可知,导线的a端和c端看成一个点,导线的b端和d端看成一个点,这样L1、L2和L3的一端重合为一个点,另一端重合为另一个点,由此可知,该电路有三条支路,并由“电流流向法”可知,电流分三条叉,因此这个电路是三盏电灯的并联,等效电路如右图所示。 ◆使用拆除法识别串并联电路 拆除法是识别较难电路的一种重要方法。它的原理就是串联电路中各用电器互相影响,拆除任何一个用电器,其他用电器中就没有电流了;而并联电路中,各用电器独立工作,互不影响,拆除任何一个或几个用电器,都不会影响其他用电器。 如图所示,两个灯泡通过灯座装在一个木匣子上,A、B、C、D分别是连接两灯泡灯座的接线柱。E、F两接线柱间接上电源后,两灯泡发光。如何判断两灯泡是串联还是并联? 分析:串联电路只有一个电流的路径,只要一处断开,整个电路断路,即其他用电器不能工作;并联电路有两个或两个以上电流的通路,其中一个支路断开,其他支路的用电器仍然工作,即各用电器件互不影响。因此可用断路法进行判断。 |