|
高二是承上启下的一年,也是最容易出现动荡和茫然的时期,暑假是弯道超车的好时机,抓紧提前学吧!下面是小编给大家带来的新高二上册所学教材必修3预习,算法的案例知识点梳理,一起高效学习,跨越高二分水领吧!  一 辗转相除法&更相减损法 辗转相除法 用辗转相除法求最大公约数的算法步骤: ①给定两个正整数m,n(m>n) ②计算m除以n所得的余数r ③赋值m=n,n=r ④若r=0,则m,n的最大公约数等于m;否则,返回第②步 程序框图:  例题:求8251跟6105的最大公约数 解: 8251=6105x1+2146(余数为2146) 6105=2146x2+1813(余数为1813) 2146=1813x1+383(余数为383) 1813=383x5+148(余数为148) 383=148x2+37(余数为37) 148=37x4(余数为0) ∴8251跟6105的最大公约数为37 更相减损法 用更相减损法求最大公约数的算法步骤: ①给定两个正整数m,n(m>n) ②若m,n都是偶数,则不断用2约简,使得他们两个不同时是偶数,约简的两个数仍记为m,n ③计算m-n所得的差d ④判断“d不等于n“是否成立,若是,则将n,d中较大者用m表示,较小者用n表示,返回第③步;否则2k·d(k是约简整数2的个数)为所求的最大公约数。 例题:用更相减损法求98与63的最大公约数 解: 98-63=35 63-35=28 35-28=7 28-7=21 21-7=14 14-7=7 ∴98与63的最大公约数为7 辗转相除法与更相减损术的区别 ①两种方法都是求最大公约数,计算上辗转相除法以除法为主,更相减损术以减法为主,计算次数上辗转相除法计算次数相对较少,特别当两个数字大小区别较大时计算次数的区别较明显。 ②从结果体现形势看,辗转相除法体现结果是以相除余数为0而得到,而更相减损法则是以减数和差相等而得到 二 秦九韶算法 秦九韶算法的步骤如下: 把一个n次多项式f(x)=anxn+an-1xn-1+……+a1x+a0改写成如下形式: 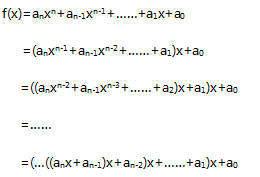 求多项式的值时,首先计算最内层括号内一次多项式的值,即 v1=anx+an-1 然后由内向外逐层计算一次多项式的值,即 v2=v1x+an-2 v3=v2x+an-3 …… vn=vn-1x+a0 这样求n次多项式f(x)的值转化为求n个一次多项式的值。 例题:f(x)=5x5+2x4+3.5x3-2.6x2+1.7x-0.8,求f(5)的值。 解: 根据秦九韶算法,题目中的多项式可以改写成如下形式: f(x)=((((5x+2)x+3.5)x-2.6)x+1.7)x-0.8 按照由内到外的顺序,依次计算一次多项式当x=5时的值: v0=5 v1=5x5+2=27 v2=27x5+3.5=138.5 v3=138.5x5-2.6=689.9 v4=689.9x5+1.7=3451.2 v5=3451.2x5-0.8=17255.2 ∴当x=5时,多项式的值等于17255.2 秦九韶算法的程序框图: 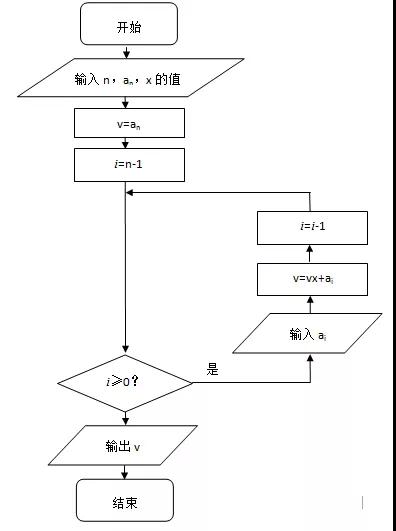 三 进位制 定义: 进位制是一种记数方式,用有限的数字在不同的位置表示不同的数值。例如二进制就是满二进一,十进制就是满十进一,十二进制就是满十二进一等等,换句话说,满几进一就是几进制。 一般地,若k是一个大于1的整数,那么以k为基数的k进制数,可以表示为一串数字连写在一起的形式。具体如下: anan-1……a1a0(k)(0<an<k,0≤an-1,……,a1,a0<k) ①k进制转换为十进制 例题1:把二进制数110011(2)化为十进制数 解: 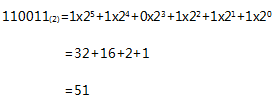 例题2:设计一个算法,把k进制数a(共有n位)化为十进制b,用程序框图表示。 解: 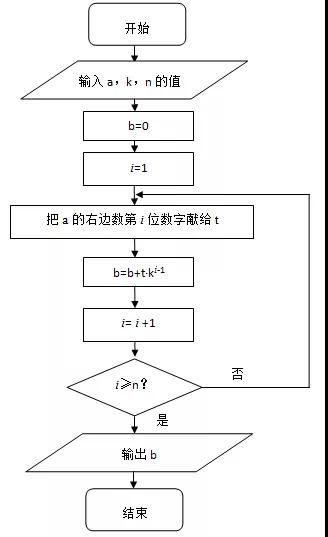 ②十进制转换为k进制 例题1:把89化为二进制的数 解: 根据二进制数“满二进一”的原则,可以用2连续去除89或所得商,然后取余数,具体计算方法如下: 89=2x44+1 44=2x22+0 22=2x11+0 11=2x5+1 5=2x2+1 2=2x1+0 1=2x0+1 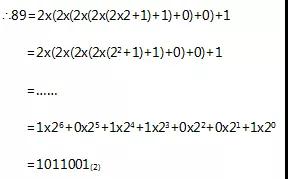 这种算法叫做除2取余数法,还可以用下面的除法算式表示: 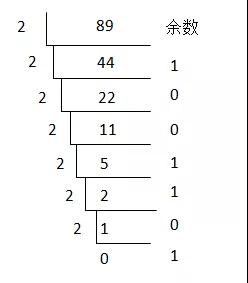 把上式中各步所得的余数从下到上排列,得到89=1011001(2) 上述方法也可以推广为把十进制数化为k进制数的算法,称为除k取余法。 例题2:设计一个算法,用除k取余法,将十进制a化成k进制,用程序框图表示。 解: 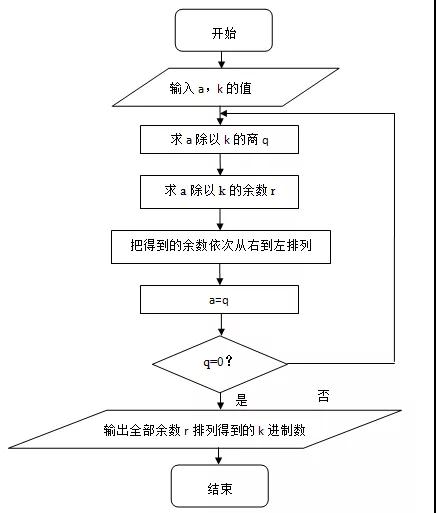 (责任编辑:admin) |
