|
高中家教班老师为大家整理了高中数学必修五第三章不等式的知识点,高二的同学们积极备战期末考试! 近年来在高考解答题中,常渗透不等式证明的内容,而不等式的证明是高中数学中的一个难点,它可以考察学生逻辑思维能力以及分析问题和解决问题的能力。特别值得一提的是,高考中可以用“放缩法”证明不等式的频率很高,它是思考不等关系的朴素思想和基本出发点, 有极大的迁移性,对它的运用往往能体现出创造性。  一,添加或舍弃一些正项(或负项)   二,先放缩再求和(或先求和再放缩) 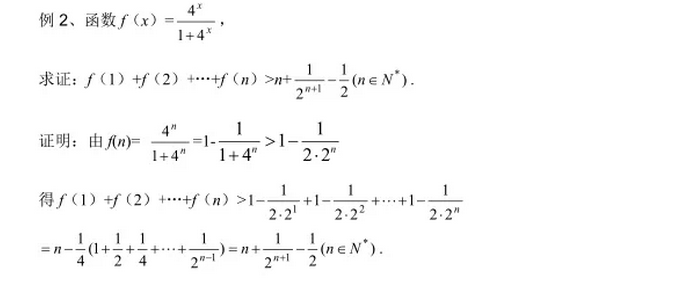 三,先放缩,后裂项(或先裂项再放缩)  四,放大或缩小“因式”  五,逐项放大或缩小  六,固定一部分项,放缩另外的项  七,利用基本不等式放缩  八,先适当组合, 排序, 再逐项比较或放缩  以上介绍了用“放缩法”证明不等式的几种常用策略,解题的关键在于根据问题的特征选择恰当的方法,有时还需要几种方法融为一体。在证明过程中,适当地进行放缩,可以化繁为简、化难为易,达到事半功倍的效果。但放缩的范围较难把握,常常出现放缩后得不出结论或得到相反的现象。  因此,使用放缩法时,如何确定放缩目标尤为重要。要想正确确定放缩目标,就必须根据欲证结论,抓住题目的特点。掌握放缩技巧,真正做到弄懂弄通,并且还要根据不同题目的类型,采用恰到好处的放缩方法,才能把题解活,从而培养和提高自己的思维和逻辑推理能力,分析问题和解决问题的能力。希望大家能够进一步的了解放缩法的作用,掌握基本的放缩方法和放缩调整手段。 (责任编辑:admin) |
