|
摘要：纵观近几年的全国中学生物理竞赛试题，笔者发现，对于高等数学中可以使用积分来进行计算的一些问题却在竞赛中频频出现，由于中学生在数学知识上的局限，使得这些问题一般很难解决，但是如果应用积分思想和微元法，借助初等数学工具，也可以很好地解决这类问题。因此这类问题对学生的能力提出了较高的要求，许多学生对此感到十分困惑，甚至无从下手。对此，下面笔者就积分思想和微元法谈谈在一些物理竞赛试题中的具体应用和做法，以期能收到窥斑见豹之效。
关键词：积分思想 微元法 等分分割 裂项相消 极限 一、积分思想的核心和微元法的本质 积分思想的核心就是微元法，而微元法的本质是什么呢？在处理变化的事物或变化的过程时，考虑到一切变化都必须在一定的时间和空间范围内才可能实现，微元法就抓住了“变化”的这一本质特征，通过限制变化赖以发生的时间和空间来限制变化，从而将变化的事物或变化的过程转化为不变的事物或不变的过程，以实现“化变为恒”、“化曲为直”的作用。 二、积分思想和微元法解决问题的基本步骤 1．根据问题的具体情况，选取一个变量  ，并确定它的变化区间 ，要求所求未知量 应与变量的变化区间有关，且未知量在区间上具有可加性。2．化整为零，即分割。在区间 内任意插进 个分点： ， ， ， ，为了书写方便，令 ， ，使 ，将区间分成 个小区间，则第 个区间的长度 （ ）。3．近似。在区间 上选取有代表性的任一区间 进行分析处理，运用相关数学知识及物理概念、公式和规律求出所求未知量的局部量 的近似值，将表示成 的形式（ 是第个区间上的任意一点，必要时可选取特殊点，如区间端点 或 ）。在计算过程中应充分利用“以恒代变”、“以直代曲”的思想，忽略比 高阶的无穷小量。常用的近似计算公式有 ， ， ， （ ）， 等，其中均为无穷小量。4．积零为整，即求和。将所求局部量 进行累积求和，得到所求未知量的近似值，即 。在计算和式 时，应选择适当的数学方法，常用的数学方法有等分分割求和法和裂项相消求和法。5．取极限。令各个小区间的最大长度  ，当然也就要求区间数 ，求出和式的极限，得出所求未知量的准确值。三、竞赛试题例析 例1．如图1所示，半径为 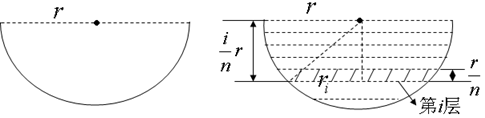 的半球形水池装满密度为 的水，要将池内的水抽干，至少要做多少功？ 图1 图2 分析与解答：按题目要求只要将水抽至水面的高度就可以了。如图2所示，将水分割成 层，且每层的厚度都为 ，即等分分割，将一层一层的水即“微元”抽至水面即可。取水面下第 层水考虑，第层水的厚度为 ，其距水面的高度可以认为是 ，则第层水的半径为 ，这层水的质量为 将这层水抽至水面所做的功为  所以将全部水抽至水面所需要做的功为 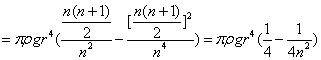  令各层水的厚度  ，即， ， 。本题计算和式时采用的是等分分割求和法，当然也可以采用裂项相消求和法，具体做法与下面的例2完全类似，请看下例。 例2．如图3所示，水平放置的金属细圆环半径为 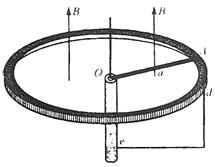 ，竖直放置的金属细圆柱（其半径比小得多）的端面与金属圆环的上表面在同一平面内，圆柱的细轴通过圆环的中心 。一质量为 ，电阻为 的均匀导体细棒被圆环和细圆柱端面支撑，棒的一端有一小孔套在细轴上，另一端可绕轴线沿圆环作圆周运动，棒与圆环的摩擦系数为 。圆环处于磁感应强度大小为 、方向竖直向上的恒定磁场中，式中 为大于零的常量，为场点到轴线的距离，金属细圆柱与圆环用导线 连接。不计棒与轴及与细圆柱端面的摩擦，也不计细圆柱、圆环及导线的电阻和感应电流产生的磁场，问沿垂直于棒的方向以多大的水平外力作用于棒的端才能使棒以角速度 匀速转动。 图3 分析与解答：将整个导体棒分割成 个小线元，小线元端点到轴线的距离分别为 第 个线元的长度为 ，当 很小时，可以认为该线元上各点的速度都为 ，各点的磁感应强度都为 ,该线元因切割磁感线而产生的感应电动势为 （1）整个棒上的感应电动势为  （2）由  略去高阶小量  及  ，可得 代入（2）式，得 （3）由全电路欧姆定律，导体棒通过的电流为  （4）导体棒受到的安培力方向与棒的运动方向相反。 第 个线元 受到的安培力为 （5）作用于该线元的安培力对轴线的力矩  作用于棒上各线元的安培力对轴线的总力矩为  ，即 （6） 因棒 端对导体圆环的正压力为 ，所以摩擦力为 ，对轴的摩擦力矩为 （7）其方向与安培力矩相同，均为阻力矩。为使棒在水平面内作匀角速转动，要求棒对于 轴所受的合力矩为零，即外力矩与阻力矩相等，设在点施加垂直于棒的外力为 ，则有 （8）由（6）、（7）、（8）式得  本题计算和式时采用的是裂项相消求和法，比等分分割求和法显得更为简便，但技巧性较强，笔者不妨再举一例。 例3．如图4所示，一个用绝缘材料制成的扁平薄圆环，其内、外半径分别为  、 ，厚度可以忽略。两个表面都带有电荷，电荷面密度 随离开环心距离变化的规律均为 ， 为已知常量。薄圆环绕通过环心垂直环面的轴以大小不变的角加速度 减速转动， 时刻的角速度为 。将一半径为 （ ）、电阻为并与薄圆环共面的导线圆环与薄圆环同心放置。试求在薄圆环减速转动过程中导线圆环中的张力 与时间 的关系。已知：半径为、通有电流 的圆线圈（环形电流）在圆心处产生的磁感应强度为 （ 为已知常量） 图4 分析与解答：用半径分别为  的  个同心圆把塑料薄圆环分割成个细圆环．第个细圆环的宽度为，其环带面积 ，式中已略去高阶小量 。该细圆环带上、下表面所带电荷量之和为  设时刻 ，细圆环转动的角速度为，则 单位时间内，通过它的“横截面”的电荷量，即为电流  由环形电流产生磁场的规律，该细圆环的电流在环心 产生的磁感应强度为 （1）式中 是一个微小量，由 ，得 （2）将各细圆环的电流产生的磁场叠加，由（1）、（2）式得出环心 点处的磁感应强度   （3） 由于 ，可以认为在导线圆环所在小区域的磁场是匀强磁场，可由点的场表示。磁场对导线圆环的磁通量 （4）由于 是变化的，所以上述磁通量是随时间变化的，产生的感应电动势的大小为 （5）由全电路欧姆定律可知，导线圆环内感应电流的大小为  （6）设题图中薄圆环带正电作逆时针旋转，穿过导线圆环的磁场方向垂直纸面向外，由于薄圆环作减角速转动，穿过导线圆环的磁场逐渐减小，根据楞次定律，导线圆环中的感应电流亦为逆时针方向，导线圆环各元段 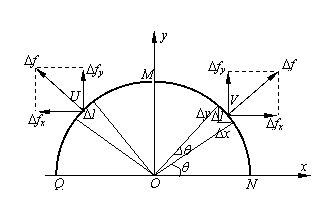 所受的安培力都沿环半径向外．现取相对于 轴两对称点 、 ，对应的二段电流元 所受的安培力的大小为 （7）  图5 方向如图5所示，它沿 及方向分量分别为 （8） （9）根据对称性，作用于沿半个导线圆环  上的各电流元的安培力的分量之和相互抵消，分量之和为 （10） 由于半个圆环处于平衡状态，所以在导线截面  、 处所受的来自另外半个圆环的张力应满足 ．由（3）、（6）两式得 “对称”是本题的特点，“微元法”是具体的解法，“对称法”也是解物理题的一种常用方法。 总之，积分思想和微元法是分析和解决高中物理竞赛试题的常用方法，也是从局部到整体的科学思维方法。运用这种思想和方法不仅丰富了处理物理问题的手段，拓展了我们的思维，还为高中阶段的后续学习奠定了思维基础。因此，对于参加物理竞赛的学生，应当深刻领会这一思想和方法并能熟练应用。 参考文献： 1．张大同编《高中物理竞赛辅导》 陕西师范大学出版社（2000年6月第2版） 2．中科大高等数学教研室编《高等数学导论》上册 中科大出版社（2007年8月第3版） (责任编辑：admin) |