|
浅析带电粒子在磁场中运动的多解问题 江苏省泰州中学 高峰 带电粒子在只受洛仑兹作用下的圆周运动考查的重点都集中在粒子在有边界的磁场中做不完整的圆周运动的情况,由于题设中隐含条件的存在,就会出现多解问题,下面通过实例对此类问题进行分析。 一、粒子的带电性质不明的情况 【例1】如图1所示,匀强磁场的磁感应强度为B,方向垂直纸面向里,MN是它的下边界。现有质量为m,电荷量为q的带电粒子与MN成30°角垂直射入磁场,求粒子在磁场中运动的时间。 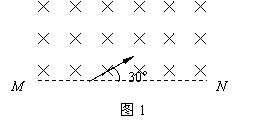 【解析】粒子在磁场中的偏转方向取决于所受的洛仑兹力的方向,不同电性的粒子所受的洛仑兹力的方向不同,本题没有明确粒子究竟带何种性质的电荷,所以粒子的轨迹可能是图2中的两条。 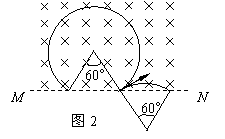 由 由图可知: 二、临界条件不唯一的情况 【例1】如图3所示,M、N是两块水平放置的平行金属板,板长为L,板间距离为d,两板间存在磁感应强度为B,方向垂直于纸面向里的匀强磁场。有一质量为m,电荷量为q的带正电粒子从磁场左侧靠近N板处水平射入,欲使粒子不能打到金属板上,则粒子的入射速度v 应满足什么条件? 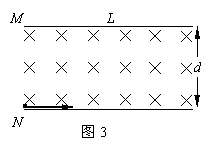 【解析】欲使粒子不能打到金属板上,则粒子可能会从磁场右侧飞出,圆周运动的半径较大;粒子也可能会从磁场左侧飞出,圆周运动的半径较小。那么粒子不会打到金属板的临界条件就有两个:粒子刚好从金属板M的右侧边缘和左侧边缘射出。其临界条件所对应的运动轨迹如图4所示。 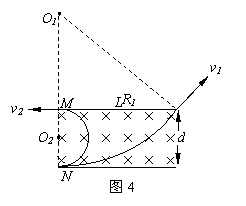 (1)粒子入射速度为v1时,轨迹半径为R1,由几何知识知: R12 = (R1-d)2 + L2 根据牛顿第二定律有: qv1B = mv12/R1 解得:v1 = qB (d2+L2) /2md (2)粒子入射速度为v2时,轨迹半径为R2,由几何知识知: R2 = d/2 根据牛顿第二定律有: qv2B = mv22/R2 解得: v2 = qBd/2m 所以粒子入射速度v 应满足的条件是: v>v1 或 v<v2 三、粒子运动的周期性引起的多解问题 【例2】如图5所示,垂直纸面向里的匀强磁场以MN 为边界,左侧磁感应强度为B1,右侧磁感应强度为B2,B1=2B2=2T,荷质比为2×106C/kg的带正电粒子从O点以v0=4×104m/s的速度垂直MN进入右侧的磁场区域,求粒子通过距离O点4cm的磁场边界上的P点所需的时间。   【解析】(1)若粒子经过P点的轨迹如图6所示, 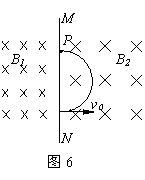  则粒子运动的时间 (2)若粒子经过P点的轨迹如图7所示, 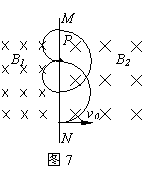  则粒子运动的时间 |
