|
辨析波动质元的振动与孤立振子的振动 江苏省南通市第二中学 陈雅 空间媒质质点的简谐振动状态在媒质中传播，便形成了简谐波，如图1所示。各质元均在自己的平衡位置附近不断振动着，振动过程中质元的位移、速度、动能和势能都发生着周期性变化，这种变化与孤立振子的振动情况何其相似！那么，事实上，在众多“相似”的表象背后，两者是否有所区别？为讨论方便和切合中学师生的理论及数学基础，本文以一维简谐振动和一维简谐波为例，从振动能量、受力和振动频率三个方面展开讨论。 1．振动能量 孤立谐振子的振动函数可以表示为 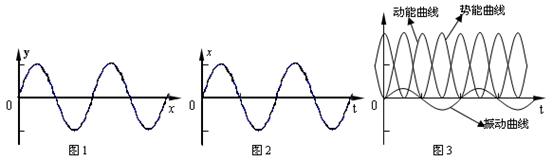 ⑴ 其中  、 、 分别为振幅、角频率和初相位。振动图像如图2所示（设=0）。由  ⑵谐振子的动能为：  ⑶势能为：  ⑷因为  ，由⑶、⑷可知，谐振子的机械能为： ⑸E是定值，所以简谐振子的机械能守恒。在两个周期内，画出动能和势能的变化图线，如图3所示。动能和势能相位差为  ，两者相互转化。而在波动过程中，振源的能量通过弹性介质传播出去，介质中各部分质元在平衡位置附近振动，介质中各部分具有动能，同时介质因形变而具有势能。波动的过程实际是能量传递的过程。 设波在体密度为ρ的弹性介质中传播，在波线上坐标x处取一个体积元  ，在时刻t，该体积元的振动位移为 ⑹其中 、、 分别为振幅、角频率和波速。上式显示，质元的振动位移由时间t和距离振源的距离x两个因素决定，如果令t固定，那就是拍下的一幅“集体照”，即波动图像；若令x固定，那就是某个质元的一段“视频”，即振动图像。另外，⑹式也表明了波动质元的振动是简谐运动。振动速度  ⑺振动动能  ⑻单位体积媒质中弹性势能等于弹性模量与应变平方乘积的一半，应变  所以体积元 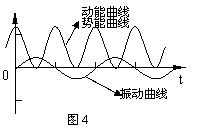的势能为 ⑼ 因为  ，所以振动势能为 ⑽振动机械能  ⑾  可见，在波动中媒质质元的机械能不是恒定的，而是随时间作周期性变化，且动能与势能每时每刻都等量同相位变化，如图4所示。在平衡位置，动能和势能都最大，机械能最大；在最大位移处，动能和势能都最小，机械能最小。质元能量从最小向最大变化的过程便是能量输入的过程，质元能量从最大向最小变化时为能量的输出过程。 2．受力与频率 孤立谐振子在振动时，不受外力的作用。以弹簧振子为例，弹簧和质点共同组成弹簧谐振子，此谐振子中的弹簧弹力为内力，不是外力。而波动的质元一方面在能量输入端受到源动力的作用，另一方面在能量的输出端又要受其他质点的阻力的作用。所以说，孤立谐振子的振动是独立的振动，其频率等于振子系统的固有频率；波动质元的振动是受迫振动，其振动频率等于振源策动力的频率，与质点媒质的固有频率无关。 由以上的讨论可以做出这样的结论：尽管波动包含振动，波动质元的振动与孤立振子的振动都是简谐振动，但是两者在能量、受力和振动频率三个方面都有所不同。尤其是关于振动能量问题，往往会认为波动中质元的能量也如孤立振动，是守恒的，在平衡位置动能最大势能最小，在最大位移处则动能最小势能最大，而实际上则不然。波动质元在平衡位置动能和势能均最大，机械能最大，在最大位移处则动能和势能都最小，两者同位相变化。 参考文献： 赵凯华、罗蔚茵，新概念物理教程力学，高等教育出版社，2001．5 (责任编辑：admin) |