|
变力做功问题的解法 河南省新县高级中学 吴国富 高中物理教材利用恒力对物体做功的物理模型推导出功的计算式  。如果力的大小是变化的，那么公式中的F就无法取值；如果力的方向是变化的，公式中 角就无法取值。因此其公式仅适用于恒力做功过程，而对于变力做功问题又经常出现，那我们该如何求解呢？本文现就计算变力所做功的方法及到底采用哪种方法进行求解作如下阐述。一、将变力处理成恒力 将变力处理成恒力的方法，一般只在力的大小一直不变，而力的方向遵循某种规律的时候才用。 例1 如图1所示，有一台小型石磨，某人用大小恒为F，方向始终与磨杆垂直的力推磨。假设施力点到固定转轴的距离为L，在使磨转动一周的过程中，推力做了多少功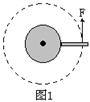？  解析：由于力F方向不断变化，因此是一个变力做功问题，如果将推力作点的轨迹分成无限多小段  ，每一段曲线近似为直线，力F的方向也近似与这一小段的轨迹重合，则每小段均可看作恒力做功过程。运用恒力作功的计算式求出各小段推力做的功：  ．则转动一周过程中推力做的功：  。二、力的平均值法 通过求力的平均值，然后求变力的平均力做功的方法，一般是用于力的大小与位移成一维线性关系的直线运动中。 例2 如图2所示，劲度系数为 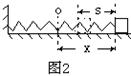 的轻质弹簧一端固定在墙上，另一端连接一质量为 的滑块，静止在光滑水平面上O点处，现将滑块从位置O拉到最大位移 处由静止释放，滑块向左运动了s米（ ）．求释放滑块后弹簧弹力所做的功。 解析：弹簧对滑块的弹力与弹簧的形变量成正比，求出弹力的平均值为：  用力的平均值乘以位移即得到变力的功：  。三、动能定理法 动能定理求变力的功是非常方便的，但是必须知道始末两个状态的物体的速度，以及在中间过程中分别有那些力对物体做功，各做了多少功。 例3 如图3所示，质量为 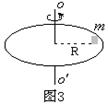的物块与转台之间能出现的最大静摩擦力为物块重力的倍，它与转轴 相距R，物体随转台由静止开始转动，当转速增加到一定值时，物块开始在转台上滑动，在物块由静止到开始滑动前的这一过程中，转台对物块做的功为多少？ 解析：由题意知物块即将滑动时受到的摩擦力为  ，设此时物块运动的速度为 ，则有 ，于是有 。由动能定理知，从静止到开始滑动前这段时间内转台对物块做功为： 。四、功能原理法 除系统内的重力和弹簧弹力之外，其它力做的功等于系统机械能的增量，即  。例4 如图4所示，一质量均匀的不可伸长的绳索重为G，A、B两端固定在天花板上，今在最低点C施加一竖直向下的力将绳拉至D点，在此过程中，绳索AB的重心位置将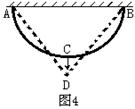（ ）  A．逐渐升高 B．逐渐降低 C．先降低后升高 D．始终不变 解析：在C点施加的竖直向下的力做了多少功，就有多少其它能转化为绳的机械能。由于  ， ，而 ，所以 ，即绳的重力势能增加，得知绳重心升高。五、图象法 表示力随位移变化规律的图象叫做示功图。其纵坐标轴表示作用在物体上的力F，横坐标轴表示力的作用点在力的方向上的位移s。图象、力轴、位移和由位移决定的与力轴平行的直线所围成的面积在数值上等于变力所做的功。 例5 如图5所示，一个劲度系数为 的轻弹簧，一端固定在墙壁上，在另一端沿弹簧的轴线施一水平力将弹簧拉长，求在弹簧由原长开始到伸长量为x1过程中拉力所做的功。如果继续拉弹簧，在弹簧的伸长量由x1增大到x2的过程中，拉力又做了多少功？ 解析：在拉弹簧的过程中，拉力的大小始终等于弹簧弹力的大小，根据胡克定律可知，拉力与拉力的作用点的位移x（等于弹簧的伸长量）成正比，即：F=kx F-x关系图象如图6所示，由图可知△AOx1的面积在数值上等于把弹簧拉伸x1的过程中拉力所做的功，即 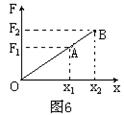  梯形Ax1x2B的面积在数值上等于弹簧伸长量由x1增大到x2过程中拉力所做的功，即  六、运用  求解当机车以恒定功率工作时，在时间  内，牵引力做的功。例6 电动机通过一绳吊起一质量为8kg的物体，绳的拉力不能超过120N，电动机的功率不能超过1200W，要将此物体由静止起，用最快的方式吊高90m所需时间为多少（已知此物体在被吊高达90m时开始以最大速度匀速上升）？ 解析：本题可分为两个过程来处理，第一个过程是以绳所能承受的最大拉力拉物体，使物体匀加速上升，第一个过程结束时，电动机的功率刚达到最大功率．第二个过程是电动机一直以最大功率拉物体，拉力逐渐减小，物体变加速上升，当拉力减小至等于重力时，物体开始匀速上升。 在匀加速运动过程中，加速度：  ，末速度： ，上升时间： ，上升高度： 在功率恒定的上升过程中，设经h2后，达匀速运动的速度：  ，此过程中外力对物体做的总功 ，由动能定理 得： ，其中h2=H-h1=80m解得  所需时间最小应为： 
(责任编辑：admin) |