|
电磁感应与电路综合题解题策略和方法 河北省鸡泽县第一中学 吴社英 知识要点： 电磁感应是电磁学的核心内容，重点研究电磁感应现象的产生条件，感应电流方向的判定，感应电动势大小的计算。交变电流是电磁感应理论的延续和具体应用。 电路部分，其一是以部分电路欧姆定律为中心，包括六个基本物理量（电压、电流、电阻、电功、电功率、电热），三条定律（部分电路欧姆定律、电阻定律和焦耳定律），以及若干基本规律（串、并联电路特点等）；其二是以闭合电路欧姆定律为中心，讨论电动势概念，闭合电路中的电流、路端电压以及闭合电路中能量的转化。 纵观近几年各种形式的高考试题，电磁感应和电路部分知识每年必考，并把电磁感应、磁场、电路以及力学中力的平衡、恒力做功等知识有机地结合，编组成电磁学和电路的综合型题较多，题型有选择题、填空题、计算题等，难度在中档左右，也有以这两部分知识命题的压轴题，复习过程中应予以高度重视，强化训练。 电磁感应中，涉及“棒生电”的命题颇多，是高考的热点、重点，也是难点。 “棒生电”指导体棒在磁场中先运动，后产生感应电动势或感应电流的问题，导体棒切割磁感线分为平动切割和转动切割两种：在匀强磁场中，B、  、 三量互相垂直平动切割磁感线时，感应电动势大小为 ；导体棒在匀强磁场中绕平行于磁感线的固定轴匀速转动时，感应电动势的大小为 。典型例题 例1 如图1所示，金属棒P从高h处以速度 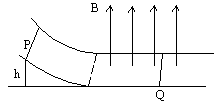 沿光滑弧形平行导轨下滑，进入轨道的水平部分后，在自下而上垂直于导轨平面的匀强磁场中运动，磁感应强度为B，在轨道的水平部分原来静止放着另一根金属棒Q，已知 ，假设导轨足够长，试问： 图1 （1）当P棒进入磁场后，P、Q棒各做什么运动？ （2）P棒刚进入磁场时，P、Q两棒加速度之比为多少？ （3）若两棒始终没有相碰，求P和Q的最大速度？ （4）在整个过程中，回路中消耗的电能是多少？ 分析：解本题的关键应抓住（1）当P、Q两棒速度相等时，回路电流为零，P、Q不受安培力做匀速直线运动；（2）P、Q两棒所受合外力为零，动量守恒；（3）全过程能量守恒。 讲解：本题所涉及的物理过程，可以分为三个阶段： 第一阶段：P棒沿光滑弧面下滑，直到进人水平轨道之前，整个系统机械能守恒，即Q棒不动，对P棒   ∴  第二阶段：P棒刚进入磁场时速度最大，其后由于P棒切割磁感线使整个回路产生感应电流，反过来由于P、Q棒中有电流存在，两棒又受安培力作用而分别做减速和加速运动，直到两棒速度相同为止，该速度即为Q棒最大速度。由于两棒所受安培力 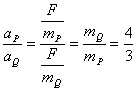 ，尽管回路中感应电流不断变化，但两棒通过的电流始终相等，所以两棒所受安培力大小始终相等，这样两棒运动加速度之比始终为 。在这一阶段中，两棒运动速度不断变化，回路中的感应电动势、感应电流、安培力、两棒的加速度都在不断地变化，用牛顿定律求两棒速度是非常困难的，但若把两棒看成一个运动系统，它们在安培力作用下速度从不同到相同的运动情况，可用动球碰静球的完全非弹性碰撞相类比，这样根据动量守恒定律  ∴  第三阶段：两棒速度相同后，穿过整个回路的磁通量不再变化，回路中无电流，两棒不再受安培力作用，在光滑水平轨道上各自做匀速运动，整个系统无能量消耗。 要计算从P棒下滑到两棒均以v滑动的全过程中回路消耗的电能，因感应电流为变量，无法用  计算，但根据能量守恒定律，回路消耗的电能即系统减少的机械能。∴   综合以上分析： （1）P棒刚进入磁场阶段，P棒做减速运动，Q棒做加速运动，随着两棒速度差的减小，两棒运动加速度也不断减少； （2）两棒加速度之比为  ；（3）P棒最大速度 ，Q棒最大速度 ；（4）整个过程回路消耗的电能  答案： （1）P棒刚进入磁场阶段，P棒做减速运动，Q棒做加速运动，随着两棒速度差的减小，两棒运动加速度也不断减少； （2）两棒加速度之比为 （3）P棒最大速度 ，Q棒最大速度；（4）整个过程回路消耗的电能 。评析：通过本例题的讲解可总结得出，受力情况、运动情况的动态分析，可按如下思考方法：电磁感应现象中产生感应电动势  感应电流通电导体受安培力合外力变化加速度变化速度变化感应电动势变化……周而复始地循环，循环结束时，加速度等于零，导体达到稳定运动状态，要画好受力图，抓住 时，速度v达最大值的特点。例2 如图2（甲）所示，一个由导体做成的矩形线圈，以恒定速率v运动，从无场区进入匀强磁场区，然后出来，若取逆时针方向为电流的正方向，那么图2（乙）中所示的哪一个图象正确地表示回路中电流对时间的函数关系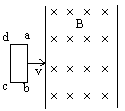？  图2（甲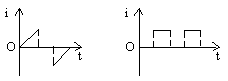）   A B C D 图2（乙） 讲解：当线圈开始运动，尚未进入磁场区时，没有感应电流产生，当ab边进入磁场，ab边切割磁感线产生的感应电动势  为定值，因此感应电流也为定值，方向为逆时针（正）。当cd边进入磁场时，ab和cd边产生的感应电动势互相抵消，没有感应电流，当线圈继续运动，在磁场中只有cd边时，又开始有感应电流，大小不变，方向为顺时针（负），cd边离开磁场后线圈无感应电流，所以C图才是正确的。评析：回路中感应电动势  、感应电流i、磁感应强度B的方向，在 图、 图、 图中是通过正负值来反映的，分析回路中的感应电动势或感应电流的大小及其变化规律，要利用法拉第电磁感应定律来分析，有些图象问题还要画出等效电路来辅助分析。例3 如图3所示，与光滑的水平平行导轨P、Q相连的电路中，定值电阻  ， ；电压表的量程为0～10V，电流表的量程为0～3A，它们都是理想电表；竖直向下的匀强磁场穿过水平导轨面，金属杆ab横跨在导轨上，它们的电阻均可不计，求解下列问题：（1）当滑动变阻器的阻值  时，用水平恒力 向右作用于ab，在ab运动达到稳定状态时，两个电表中有一个电表的指针恰好满偏，另一个电表能安全使用，试问：这时水平恒力F1的功率多大？ab的速度 多大？（2）将滑动变阻器的电阻调到 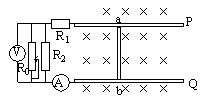 ，要使ab达到稳定运动状态时，两个电表中的一个电表的指针恰好满偏，另一个电表能安全使用，作用于ab的水平恒力F2多大？这时ab的运动速度 多大？ 图3 讲解： （1）当 时， 与 的并联阻值为 ，显然，这时电压表满偏，读数为10V，电流表读数为2A。（如果电流表指针满偏，为3A，则电压表上电压为 ，超过它的量程，不能安全使用）在这种情况下电路中感应电流的总功率为  。根据能的转化和守恒定律，F1的功率与感应电流的功率相等即为40W。 由  ，可知ab的速度 （2）当 时，它与的并联阻值 ，电路中总电阻 。显然，这时电流表指针满偏，为3A，电压表示数为6V。（若电压表指针满偏为10V，则通过电流表的电流为 ，超过它的量程不能安全使用）这时电路中感应电流的总功率，即F2的功率为  ab切割磁感线产生的感应电动势为  （因ab的电阻不计）在（1）问中，感应电动势为   由  ，可得作用于ab的恒力为 答案：（1）40W  （2）60N  评析：本题是集电磁感应、电路计算与分析、力学中的功率及能的转化和守恒定律于一体的综合性题目，要有扎实的基础知识和较强的实际分析能力才能正确的解答此题。 解题的关键是： （1）运用电路中所学知识分析出两个电表中，哪一个满偏，哪一个在安全使用，从而得到解题中所需的数据； （2）明确电磁感应现象中能的转化和守恒关系，外力克服安培力做功，把其他形式的能转化为电能，由电流的热效应转化为内能，且在转化过程中能量是守恒的。 例4 如图4所示，铜质圆盘绕竖直轴O在水平面内匀速转动，圆盘半径为 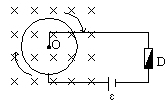 ，处在垂直纸面向里的磁感应强度 的匀强磁场中，两个电刷分别与转动轴和圆盘的边缘保持良好接触，并与电池和保险丝D串联成一闭合电路。 图4 已知电池电动势  ，电路中总电阻 ，保险丝的熔断电流为1A，试分析计算：为了不使保险丝烧断，金属圆盘顺时针方向转动的角速度的取值范围是什么？讲解：圆盘不动时，电路电流  ，大于保险丝的熔断电流，保险丝将被烧断。圆盘顺时针方向转动时，相当于长度为r的导体在垂直于磁场的平面里绕O轴以角速度  匀速转动，感应电动势大小为 ①圆盘边缘电势比转动轴处电势高，在闭合电路中感应电动势的方向与电池电动势的方向相反，要保险丝不被烧断，在转动角速度较小时要满足  ②在转动角速度较大时应满足  ③把数据  代入①②③解得 再把数据  代入上式解得 答案： 评析：在求解此题时，要注意到在转动角速度较小时，电池电动势 将大于感应电动势 ，电流将在电路顺时针方向流动；在转动角速度较大时，感应电动势大于电池电动势，电流在电路中逆时针方向流动。例5 如图5所示，da、cb为相距 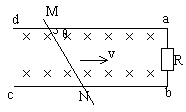的平行导轨（电阻可以忽略不计），a、b间接一个固定电阻，阻值为R，长直细金属杆MN可以按任意角 架在平行导轨上，并以匀速v滑动（平移），v的方向和da平行，杆MN有电阻，每米长的电阻值为R，整个空间充满匀强磁场，磁感应强度的大小为B，方向垂直纸面（dabc平面）向里。 图5 （1）求固定电阻R上消耗的电功率为最大时 角的值。（2）求杆MN上消耗的电功率为最大时 角的值。讲解：如图5所示，杆滑动时切割磁感线而产生感应电动势为 ，与角无关。用r表示两导轨间那段杆的电阻，回路中的电流为  （1）电阻R上消耗的电功率为  由 和R均与无关，所以r的值最小时 的值达最大，当杆与导轨垂直时两轨道间的杆长最短，r的值最小，所以最大时的值为 。（2）杆上消耗的电功率为  要求 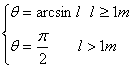 最大，即要求 取最大值。由于 显然，  时，有极大值，因每米杆长的电阻值为R，即要求两导轨间的杆长为1m，所以有以下两种情况：① 如果  ，则满足下式时  所以  ②如果  ，则两导轨间那段杆长总是大于1m，即总有 ，由于 在 的条件下，上式随r的减小而单调减小，r取最小值时， 取最小值，取最大值，所以取最大值时值为。答案：（1） （2） 评析：该题体现了数学方法在分析解答物理问题上的重要作用。 例6 如图6所示，电动机通过其转轴上的绝缘细绳牵引一根原来静止的长为 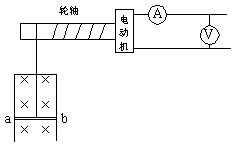 ，质量 的导体棒ab，导体棒紧贴在竖直放置、电阻不计的金属框架上，导体棒的电阻，磁感强度的匀强磁场方向垂直于导体框架所在平面，当导体棒在电动机牵引下上升 时，获得稳定速度，此过程中导体棒产生热量 。电动机工作时，电压表、电流表的读数分别恒为7V和1A，电动机的内阻 ，不计一切摩擦， ，求： 图6 （1）导体棒所达到的稳定速度是多少？ （2）导体棒从静止到达稳定速度的时间是多少？ 讲解：电路给电动机提供一定的电功率  ，一部分损耗在电机的内阻发热上，剩余的即电机输出功率用来提升棒ab。据  ，知电机输出功率一定，棒在拉力F作用下上升，做加速度a逐渐变小的加速运动，当，即 时棒速稳定。（1）设棒达到稳定速度为v， 则有：  ①而：  ②而将数值代入①②联立解得：  （2）设棒从静止到达稳定速度用时为t，电动机的输出功等于ab棒机械能的增加量与此过程导体棒产生的热量Q之和，有：  求得 答案：（1）  （2） 评析：该题是一道综合性很强的习题。在分析物理过程中，根据题给信息“电动机通过绝缘细线牵引一棒切割磁感线”，抓住能的转化与守恒这一主线，将“电动机工作电路问题”、“机车运动问题”和“电磁感应中能的转化”的解题思路迁移过来，综合分析解决问题。 (责任编辑：admin) |