|
正确处理振动和波动的内在关系 重庆市丰都中学 付红周 一、波的形成与传播过程 1．波是波源的振动形式在介质中的传播过程，介质中的每个质点只在自己的平衡位置振动，并不随波迁移。 2．在波的传播方向上相距波长整数倍的两质点，振动起来后的情况完全相同，相距半个波长奇数倍的两质点振动情况总是相反。 3．介质中任何一个质点的起振方向总是与波源的起振方向相同，且滞后于波源的振动。 4．波速由介质决定，频率由波源决定，同一介质中波速相同，与波长和频率无关。 二、振动图象和波动图象的区别和联系 1．区别
2．联系：振动是一个质点随时间的推移而呈现的现象，波动是全部质点联合起来共同呈现的现象，简谐运动和其引起的简谐波的振幅、频率相同；图象的形状是正弦（或余弦）曲线。 三、横波的传播方向和质点的振动方向的关系 1．带动法（特殊点法） 如图，为一沿x轴正方向传播的横波，判定图上P点的振动方向。 在P点的附近靠近波源的一方的图线上另找一点P/，若P/在P的上方，P/带动P向上振动，P向上振动；若P/在P的下方，则P/带动P向下振动，P向下振动。 2．微平移法 沿波的传播方向将波的图象进行微小平移，然后由两条波形曲线来判定，如上图A/B/C/D/是ABCD运动后的位置，所以AB向上运动，CD向下运动。 3．上下坡法 沿波的传播方向看，上坡的质点向下振动，下坡的质点向上振动，即“上坡下，下坡上”下图中AC在上坡上，向下振动，B在下坡上，所以向上振动，    4．刮风法 设风沿波的传播方向刮，则风吹的地方，草被刮倒向下运动，背风的地方，风刮不到草则向上生长，即向上运动。 5．逆复描法 逆着波的传播方向，沿波形图线复描，凡提笔经过的点向上振动，凡向下拉笔的点向下振动。 例1 一列简谐波在t=0时的波形如图1所示，图2表示该波传播介质中某个质点此后一段时间内的图象，则（ ） A．若波沿轴正方向传播，图2为a点的振动图象 B．若波沿轴正方向传播，图2为b点的振动图象 C．若波沿的负方向传播，图2为c点的振动图象 D．若波沿的负方向传播，图2为d点的振动图象，     解：在图2的的图象中，t=0时刻，质点在平衡位置并向轴的正方向运动，而图1的波形却表明在t=0时刻，质点b、d才在平衡位置，而a、c不在平衡位置，所以A、C不正确；若波沿x轴正方向传播，可知质点b向上运动，B对，同理，波向x轴负方向传播，质点d向上振动，D对。 例2 一列简谐横波在t=20s时的波形如上图甲，乙是这列波中P点的振动图象，那么该波的传播速度和传播方向是（ ） A．v=25cm/s，向左传播 B．v=50cm/s，向右传播 C．v=25cm/s，向右传播 D．v=50cm/s，向左传播 解：由振动图象知T=2s，由波动图象知λ=100cm，由  ，由振动图象， 时，P质点正经过平衡位置向上振动，说明P的右方的质点早一些振动所以波向左传播，选D。例3（07四川）图甲为一列简谐横波在某一时刻的波形图，图乙为质点P以此时刻为计时起点的振动图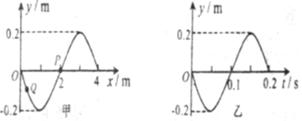（ ）  A．经过0．35 s时，质点Q距平衡位置的距离小于质点P距平衡位置的距离 B．经过0．25 s时，质点Q的加速度大于质点P的加速度 C．经过O．15 s，波沿x轴的正方向传播了3m D．经过o．1 s时，质点Q的运动方向沿y轴正方向 解：由图象知周期为0．2s，波长为4m  ，由振动图知，P向下振动，故波向右传播，波在0．15内传播的距离为 ，C对，0．35秒时P在波峰Q不在波峰，所以A对，0．25秒时，P的位移大于Q的位移，所以P的加速度大于Q，B错，0．1秒时P在平衡位置，A在平衡位置上方向下振动，D错。四、机械波的多解 1．传播方向的双向性产生多解 例4 一列横波在X轴上传播，t1=0和t2=0．005S的波形如下图所示的实线和虚线，求（1）设周期大于t2-t1，求波速。（2）设周期小于t2-t1，且 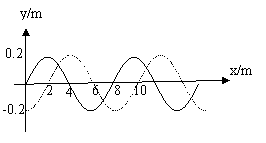 ，求波的传播方向。  解：因△t= t2-t1<T，所以波传播的距离可以直接，由图读出，若波向右传播，则在0．005s内传播了2米，则v右=  ，若波向左传播，则左0．005内传播了6m，则，v左=  ，(2)△t= t2-t1>T，所以波传播的距离大于一个波长，在0．005S内传播的距离 ， 即 ，故波向x轴负向传播。2．图象的时间周期性和空间周期性形成多解 例5 一列横波在某时刻的波形如图中实线1，经2×10-2s后的波形如图中虚线2，则波速和频率可能是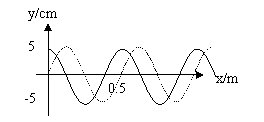（ ）   A．V=5m/s B．V=45m/s C．f=50HZ D．f=37．5HZ 解：由图可知，λ=0．4m，若波向左传播，传播的最小距离为0．3m，若波向右传，传播的最小距离为0．1m，考虑到波传播的时空周期性，则这列波传播的距离可能是S1=nλ+  λ=(0．4+0．3)m，S2=nλ+ λ=（0．4+0．1）m，（n=0，1，3…）周期可能  (n=0，1，2…）由  得 ，  ，  (n=0，1，2…）今n取不同值得出A、B、D三选项都正确。 3．波长的不确定性等形成波的多解 例6（1996年全国卷）如图甲所示，一根张紧的水平弹性长绳上的a、b两点，相距14．0m。b点在a点右方，当一列简谐波沿此绳向右传播时，若a点位移达到正向极大时，b点位移恰好为零，且向下运动。经过1．00s后，a点位移为零，且向下运动，而b点的位移恰好达到负向极大，则这列简谐波的波速可能等于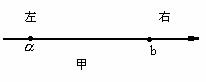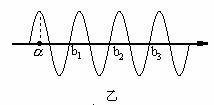（ ）   A．4．67m／s B．6m／s C．10m／s D．14m／s 分析：此题虽然已说明了波的传播方向，但满足题设条件的a、b两点可以有无数个可能位置，图乙中的b1．b2．b3……等。只可以写出a、b间距的通式；  （n＝0、1．2……）。从而波速的答案也是系列解答，经求解可知A、C为正确答案。纵观以上例子，可以看出，求解波的多解题，首先判断波的传播方向，看是否以向传播，其次，根据波形及传播方向，列出波沿不同方向传播时可能传播距离和周期的通式，再次，看质点间隐含的不同波长的关系，列出波点的通式，再分别将n=0，1，2……代入通式既可求得所有可能的答案，从而真正做到正确求解，防止漏解或用特解代通解。 练习： 1．一列简谐横波沿x轴正方向传播，某时刻(t=0)其波形如图所示，a、b、c、d是四个质元，振幅为A。下列说法中正确的是（ ） A．该时刻以后，质元a比质元b先到达平衡位置 B．该时刻以后的  周期内，质元a通过的路程为1mC．该时刻以后的  周期内，质元b通过的路程比质元c通过的路程大D．该时刻以后的  周期内，质元d通过的路程等于A2．如图甲所示是t =1．0 s时沿 x 轴负方向传播的平面简谐波的图象，已知波速v =1．0m/s．则x =1．0m处的质点的振动图象是图乙中的（ ） 
(责任编辑：admin) |
