|
运动的合成与分解问题的思路与方法 陕西省宝鸡市陈仓区教育局教研室 邢彦君 分析与求解运动合成与分解问题，就是由分运动的速度（或加速度、位移）求出合运动的速度（或加速度、位移），或者由分运动的速度（或加速度、位移）求出合运动的速度（或加速度、位移）。分析与求解的思路与方法可概括为：一个法则，两个原则；一个分清，四个注意。 一、一个法则 一个法则，就是分运动的速度（或加速度、位移）与合运动的速度（或加速度、位移）之间，满足平行四边形定则。若以表示分运动的速度（或加速度、位移）矢量为邻边做平行四边形，则平行四边形的对角线就是表示合运动速度（或加速度、位移）的矢量，这是运动的合成；若以表示合运动的速度（或加速度、位移）矢量为对角线，沿分运动速度（或加速度、位移）方向做出邻边构成平行四边形，则平行四边形的邻边就是表示两个分运动速度（或加速度、位移）的矢量，这是运动的分解。 二、两个原则 一个原则，就是分解运动（速度、加速度、位移）时，遵守按效果分解的原则。就是按实际运动造成的两个运动效果确定分运动的方向。比如，在距离水平地面h高度处，将一小球以初速度vo沿水平方向抛出，它将沿图1中的虚线所示曲线落在抛出点前方的地面上某点。小球在空中的运动，造成两方面的运动效果，一是物体沿水平方向前进了l距离，二是物体在竖直方向下降了h，由于这两个运动是同时进行的，使得小球的实际运动就是沿图中虚线所示曲线轨迹的运动，一边前进一边下落。研究被水平抛出物体的运动时，按照这个效果，可将小球的运动分解为水平方向和竖直方向的两个直线运动。  另一个原则，就是简化原则。是指将一个复杂的运动分解为两个较简单的运动。比如将曲线运动分解为两个直线运动分别研究；再比如将复杂的直线运动分解为两个较简单的直线运动，如可将初速度不为零的匀加速直线运动，分解为以初速度为速度的匀速直线运动和初速度为零的匀加速直线运动。 三、一个分清 一个分清，是指运动分解时，分清楚哪个运动是合运动？哪个运动是分运动？一般来说，质点实际进行的运动，也就是我们看到的运动是合运动，与这个运动的两个运动效果相对应的运动是分运动。比如，图1中小球沿曲线的运动是合运动，水平方向与竖直方向的运动是分运动。 四、四个注意 1．注意合运动与分运动等时性：两个分运动的时间与合运动的时间相等。即合运分运动同时发生同时结束。 2．注意分运动的独立性：一个分运动的速度、加速度、位移不受另一分运动的影响。 3．注意合运动与分运动的等效性：合运动与两个分运动是等效的。可以用合运动替代两个分运动，也可用两个分运动替代合运动。 4．注意运动量的矢量性：描述合运动、分运动的物理量，如速度、加速度、位移，都是矢量。运用平行四边形法则分析求解合运动或分运动的速度、加速度、位移时，不但要求出大小还要求出方向。 五、研究运动的合成与分解问题举例 1．典型的运动合成问题——小船渡河 小船度河时，同时参与两个运动，一是相对水面的横渡运动，二是随水的漂流运动，这两个运动的合运动，就是船相对于河岸（大地）的运动，也就是岸上观察者看到的实际运动。 例1．小船在宽度为200m的河横渡，水的流速是v1=2m/s，船在静水中的速度是v2=4m/s。 （1）要使船渡河的航程最短，船应如何渡过？ （2）要使船渡河的时间最短，船应如何渡过？ 解析：（1）船的航程，就是渡河过程中相对于河岸的位移大小，也就是小船合运动位移的大小。当小船的实际航向，即合速度方向垂直河岸时航程最短，等于河宽。欲使小船合速度方向垂直河岸，由平行四边形法则可知，小船相对水面的速度方向应斜向上游。设小船相对水面的速度方向与河岸的夹角为θ时，合速度的方向恰好与河岸垂直，如图2所示。由平行四边形定则可知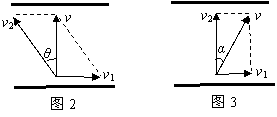：  ，代入数据解得： 。所以，当船头沿与河岸成60o斜向上游横渡时，航程最短。渡河时间为： ，而 ，代入数据解得： 。 （2）欲使小船渡河时间最短，由分运动与合运动的等时性可知，只要使任一分运动的时间最短即可。由于小船相对水面分运动速度恒定，当这一分运动的位移最小时，渡河时间最短。当小船相对水面的速度垂直河岸时，这一分运动的位移最小，等于河宽d，如图3所示。所以，渡河的最短时间为：  。小船向下游漂流的距离为： 。小结归纳：当小船相对水面的速度方向垂直河岸时，渡河时间最短。当小船相对水面的速度大于水的流速时，小船沿斜向上游一定角度航行，可使合运动的速度方向垂直河岸，航程最小。当小船相对水面的速度小于或等于水的流速时，小船沿斜向上游一定角度航行，也可使渡河的航程（和运动的位移）最小，但合运动的速度方向不会垂直于河岸，最短航程大于河宽。 2．运动分解的典型问题——牵连运动问题 一个物体通过绳子牵引另一物体运动，或者一个物体通过连杆带动另一物体运动，两物体运动方向不在一条直线时，两物体的速度大小不相等，如果按牵引或推动运动的效果，将牵引物体或带动物体的速度分解，或将两物体的速度同时分解，其中一个分速度的大小等于被牵引或推动物体的速度大小，或者一个物体的某个分速度等于另一物体的某个分速度。 例2．如图4所示，人在岸上以速度vo匀速直线前进，通过定滑轮牵引水面上的小船A靠岸。求：当绳子与水平方向的夹角为θ时，小船运动的速度大小。 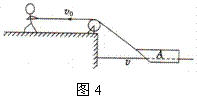  解析：将小船视为质点，它被牵引后沿水面的运动，造成两个效果，一是使绳子与竖直方向的夹角变小，相当于绳子绕定滑轮顺时钟转动，小船具有垂直于绳子斜向下的分速度。二是使定滑轮右边的绳子变短，相当于绳子与小船的连接点沿绳子斜向上运动，小船具有沿绳斜向上的分速度。如图5所示，可将小船的速度v分解为垂直绳子斜向下的速度v1和沿绳子斜向上的速度v2。由于绳子不收缩，也没被拉断，小船的分速度v2等于岸上拉绳人的速度vo，即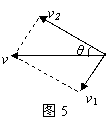：  。当绳子与水平方向的夹角为θ时，由平行四边形法则有： 。解得： 。  小结归纳：分析求解牵引或带动运动问题，一是正确辨析合运动与分运动；二是依据合运动的效果确定分运动的方向；三是寻找出两物体合速度或分速度间的相等量，一般来说，绳（或杆）两端沿绳（或杆）方向的速度相等。 (责任编辑：admin) |