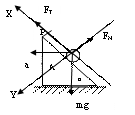
|
多矢在轴，事半功倍 辽宁省大连市103中学 姜启友 摘要：力学的许多问题都需要建立直角坐标系来解决，关于如何建系的问题，有人分了一般及特殊两种情况进行阐述。本文试图从解方程方便的角度对这两种情况进行归纳、整合，以提高学生解决问题的效率和成功率。 关键词：建系 多矢在轴 牛顿第二定律是力学的基本规律，是力学的核心知识，在整个物理学中占有非常重要的地位，是高考命题的热点。近几年来的高考物理试题，每年都有涉及本专题的知识，各种题型均有，侧重于考查物体的受力和运动情况的分析及计算，而且与实际联系紧密。在利用牛顿第二定律解决问题时，往往需要利用正交分解法建立坐标系（一般情况下坐标轴的正方向与加速度方向一致），列出牛顿运动定律方程进行求解，以往的很多材料上介绍正交分解法的解题步骤时也常常是这样的： 1、确定研究对象 2、进行正确的受力分析 3、建立坐标系 a、若a＝0 则使尽可能多的力落在坐标轴上 b、若a≠0则沿加速度方向建立x轴 4、分解不在坐标轴上的力 5、列式求解 为什么要这样建系呢？因为高中学生所接触的物理模型，一般在加速度方向上的未知矢量最多，而如果坐标轴与未知矢量重合，在列方程时，就会只在x轴的方程中或只在Y轴的方程中出现未知数。如果坐标轴与未知矢量不重合，就会既在x轴的方程中又在Y轴的方程中同时出现未知数，这样就会给求解方程造成困难，所以上述建系方法一般情况下会给求解方程带来方便。那么在加速度方向未知矢量不是很多的情况下，是否可以考虑不在加速度方向，而在有较多的未知矢量方向建立直角坐标系，列方程求解？ 请看下面的例题 例1：如图所示，车厢中有一倾角为37°的斜面，斜面上的物体A质量为1kg，当火车以10m/s2加速度沿水平方向向左运动时，物体与车厢相对静止，分析物体A所受摩擦力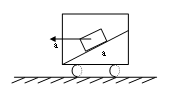．  解：对A受力分析，A受三个力作用：重力mg，弹力FN，静摩擦力Ff，设静摩擦力Ff沿斜面向上 1、常规方法：以加速度方向建立直角坐标系，如图，列方程得 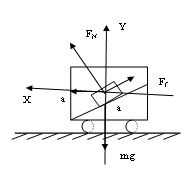  ① ②求解方程需要①×sinα-②×cosα 解得Ff = -2N为负值，说明Ff的方向与假定的方向相反，应是沿斜面向下。 2、使尽量多的未知矢量落在坐标轴上：未知矢量是弹力FN，静摩擦力Ff ，已知矢量是加速度a及重力mg，沿斜面方向建系假定A所受的静摩擦力沿斜面向上，将加速度a沿着斜面、垂直斜面正交分解，据牛顿第二定律， 沿X轴方向有：  沿Y轴方向有：   解得Ff=-2N 应是沿斜面向下。 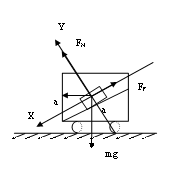 由此可见使用第二种方法，列出方程后可直接得出结论，解题过程简洁明了，提高了解题效率及准确率。 例2：如图所示，一细线的一端固定于倾角为 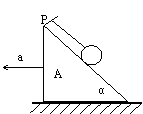 的光滑斜面顶端P，细线的另一端拴一质量为m＝1kg的小球，当滑块以加速度 向左运动时，线中的拉力为多少？ 1、常规建系方法：水平建系如图。 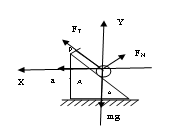  ① ②求解方程需要①×cosα+②×sinα  代入方程②中得 （如FN 为负值，则说明小球已经脱离斜面，需重新列方程求解，临界值问题，不述）求解过程中稍有不慎就会造成错误，费时费力，效率低下。 2、使尽量多的未知矢量落在坐标轴上：分析：A受三个力作用：重力，绳的拉力，斜面对小球的支持力，未知矢量是绳的拉力及斜面对小球的支持力，已知小球的加速度，所以考虑沿斜面方向建系如图，将加速度a沿着斜面、垂直斜面正交分解，列方程得：
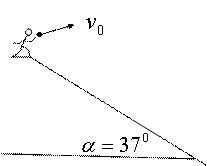
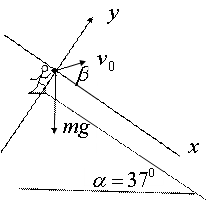
   这种方法列方程，使解方程的过程得到简化，提高解题效率，事半功倍。 例3：一人站在足够长的斜面上，斜面与水平面的夹角为 ，以速度大小为 抛出一个小球，方向未知，求小球以什么方向抛出时射程最远在这个问题当中我想如果按照常规方法分析斜抛运动水平竖直建系的话方程将会相当麻烦（在这里我不加以证明），这个问题当中未知量是位移和初速度速度不断变化，不可能按速度方向建系而按照使尽量多的未知矢量落在坐标轴上的原则应该沿着斜面方向即沿着未知量是位移方向建系。
 解：设  与斜面的夹角为 ，沿斜面方向建系如图：
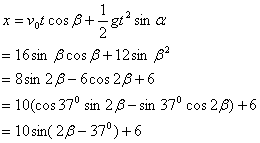 列方程得：  ① ② ③ ④由③得：  代入④中 由此可见，当  时射程最远，最远射程为16m。由以上论证可知建系列方程要考虑尽量给解方程带来方便。要想解方程方便，就要考虑使尽量多的未知矢量落在坐标轴上。在加速度方向上未知矢量不是很多的情况下，应在有较多的未知矢量方向建立直角坐标系，列方程求解，这样解方程会更加方便。而在教学过程当中，应引导学生不断地思考，体会，进而总结归纳，提高同学解题效率及成功率，从而提高同学学习物理的兴趣。在今后学习电场，磁场过程当中，也会涉及到利用牛顿第二定律列方程，大家不妨验证一下本文的观点。 (责任编辑：admin) |
