|
整体法求解共点力平衡问题举例 陕西省宝鸡市陈仓区教育局教研室 邢彦君 如果连接体中各物体的加速度相同，可以把连接体视为一个整体，整体的质量等于个物体质量的总和。此时分析连接体所受的外力，就不会出现连接体中个物体间的作用力，可以简化问题的分析与求解。 一、整体法的运用 当连接体处于静止或匀速直线运动时，各物体的加速度都是零，所以，问题若不涉及各物体间的作用力，可将连接体视为整体运用共点力的平衡条件分析求解。 例1．如图1所示，质量虽分为m1、m2的两个物体通过轻弹簧连接，在力F的作用下一起沿水平方向做匀速直线运动（m1在地面，m2在空中），力F与水平方向成θ角。则m1所受支持力N和摩擦力f正确的是 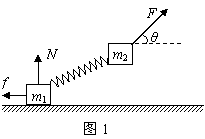 A．  B． C．  D． 解析：两物体均处于匀速直线运动状态，加速度都等于零，由于题中不涉及两物体间的作用力（弹簧的力），可将两物体视为整体，整体受力情况如图2所示。对整体运用共点力平衡条件有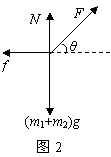：  水平方向：  ；竖直方向：  。解得： ；。本题选AD。例2．如图2所示，质量为m滑块Q沿质量为M的斜面P匀速下滑，斜面P静止在水平地面上，则在滑块Q下滑过程中地面对斜面P的  A．摩擦力方向向右，支持力大小为  B．摩擦力为零，支持力大小为 C．摩擦力为零，支持力小于 D．摩擦力方向向右，支持力小于 解析：题中不涉及滑块与斜面间作用力的分析与判断，两者的加速度都是零，所以可以将斜面与滑块视为整体，竖直方向上整体受重力 及地面支持力N的作用；水平方向上没受到外力（除地面静摩擦力以外的力）的作用，整体没有相对地面滑动的趋势，所以，地面对整体（斜面与地面的接触部分）没有静摩擦力的作用。由共点力平衡条件可知： ，解得： 。本题选B。二、整体法与隔离法的综合运用 如果问题涉及到连接体与外界物体间作用力的分析与判断，又涉及各物体间的作用力的分析与判断，可先将连接体视为整体，分析判断出与外界的作用力，再从连接体中选取涉及到要分析的力的物体中受力较少的那个物体进行分析研究。 例3．有一直角支架AOB，AO水平放置，表面粗糙，OB竖直向下，表面光滑。AO上套有小环P，OB上套有小环Q，两环质量均为m，两环间由一根质量可忽略、不可伸长的细绳相连，并在某一位置平衡（如图4所示）。现将P环向左移动一小段距离，两环再次达到平衡，那么将平衡后的状态和原来的平衡状态比较，AO杆对P环的支持力N和细绳上的拉力T的变化情况是 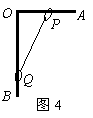  A．N不变，T变大 B．N不变，T变小 C．N变大，T变大 D．N变大，T变小 解析：由于要比较力大小的两次，两环均处于平衡状态（加速度为零，处于静止状态），故可以两环作为一个整体来研究。杆OB光滑，不会对整体（Q部分）有竖直方向的摩擦力，杆AO对整体（P部分）的支持力（弹力）垂直杆AO向上，即竖直向上。故整体在竖直方向只受重力和杆AO的支持力作用，由于两环处于平衡状态，故AO杆对P环的支持力N等于整体的重力，保持不变。对于细绳的拉力，必须把两环隔离讨论，这样，拉力才能成为外力。选环Q进行研究，它受杆OB的弹力F、重力mg、细线拉力T三力作用而处于平衡状态，按共点力的平衡条件，若把表示这三个力的矢量，保持原方向不变平移使其首尾相接，必形成封闭三角形。原先两环平衡时力矢量T与F的交点为a，将环P左移后，重力大小及方向均不变，杆OB对Q的弹力方向不变（水平），两环重新平衡时，细绳上的拉力方向与竖直方向的夹角减小，力矢量T末端左移变为T/，它与力矢量F的交点变为了b，如图5所示。由图可以看出T/小于 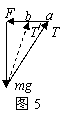 ，故T变小。本题选B。  例4．在粗糙水平地面上与墙平行放着一个截面为半圆的柱状物体A， A与竖直墙之间放一光滑圆球B，整个装置处于静止状态。现对B加一竖直向下的力F，F的作用线通过球心，设墙对B的作用力为F1，B对A的作用力为F2，地面对A的作用力为F3。若F缓慢增大而整个装置仍保持静止，截面如图6所示，在此过程中   A． F1保持不变，F3缓慢增大 B． F1缓慢增大，F3保持不变 C．F2缓慢增大，F3缓慢增大 D．F2缓慢增大，F3保持不变 解析：由于F缓慢增大的过程中，A、B一直处于静止状态，可将其视为整体。在竖直方向运用共点力平衡条件可知，F增大时，整体（A）对地面的压力增大，由牛顿第三定律可知地面对A的作用力N增大。将F分解为沿水平向左与沿BA球心方向的分力，当F增大时，两个分力都增大，由牛顿第三定律可知，F的水平分力的反作用力F1也增大，而F1的增大必然引起地面对A的静摩擦力f增大（对整体在水平方向运用共点力平衡条件）。以B为研究对象，运用共点力平衡条件可判知，B对A的作用力F2增大，这样，地面对A的作用力  也增大。本题选C。
(责任编辑：admin) |