|
2.4抛物线 重难点：建立并掌握抛物线的标准方程，能根据已知条件求抛物线的标准方程；掌握抛物线的简单几何性质，能运用抛物线的几何性质处理一些简单的实际问题． 经典例题：如图, 直线y= 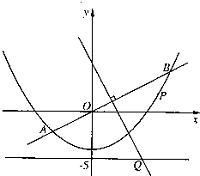 x与抛物线y= x2－4交于A、B两点, 线段AB的垂直平分线与直线y=－5交于Q点. （1）求点Q的坐标；（2）当P为抛物线上位于线段AB下方（含A、B）的动点时, 求ΔOPQ面积的最大值.  当堂练习： 1．抛物线  的焦点坐标是 （ ）A．  B． C． D．  2．已知抛物线的顶点在原点，焦点在y轴上，其上的点  到焦点的距离为5，则抛物线方程为（ ）A．  B． C． D． 3．抛物线  截直线 所得弦长等于 （ ）A．  B． C． D．154．顶点在原点，坐标轴为对称轴的抛物线过点(－2,3)，则它的方程是 （ ） A．  或 B． 或 C．  D． 5．点  到曲线 （其中参数 ）上的点的最短距离为 （ ）A．0 B．1 C．  D．2 6．抛物线  上有  三点， 是它的焦点，若 成等差数列，则 （ ）A．  成等差数列 B． 成等差数列 C．  成等差数列 D． 成等差数列7．若点A的坐标为（3，2）， 为抛物线 的焦点，点 是抛物线上的一动点，则 取得最小值时点的坐标是 （ ）A．（0，0） B．（1，1） C．（2，2） D．  8．已知抛物线  的焦点弦 的两端点为 , ,则关系式 的值一定等于 （ ）A．4p B．－4p C．p2 D．－p 9．过抛物线  的焦点F作一直线交抛物线于P，Q两点，若线段PF与FQ的长分别是 ，则 （ ）A．  B． C． D． 10．若AB为抛物线y2=2px (p>0)的动弦，且|AB|=a (a>2p)，则AB的中点M到y轴的最近距离是 （ ） A．  a B．p C． a＋ p D．a－ p11．抛物线  上到其准线和顶点距离相等的点的坐标为 ______________．12．已知圆  ，与抛物线的准线相切，则 ___________．13．如果过两点  和 的直线与抛物线 没有交点，那么实数a的取值范围是 ．14．对于顶点在原点的抛物线，给出下列条件； （1）焦点在y轴上； （2）焦点在x轴上； （3）抛物线上横坐标为1的点到焦点的距离等于6；（4）抛物线的通径的长为5； （5）由原点向过焦点的某条直线作垂线，垂足坐标为（2，1）． 其中适合抛物线y2=10x的条件是(要求填写合适条件的序号） ______． 15．已知点A（2，8），B（x1，y1），C（x2，y2）在抛物线  上，△ABC的重心与此抛物线的焦点F重合（如图）（1）写出该抛物线的方程和焦点F的坐标； （2）求线段BC中点M的坐标； （3）求BC所在直线的方程.  16．已知抛物线y=ax2－1上恒有关于直线x+y=0对称的相异两点，求a的取值范围. 17．抛物线x2=4y的焦点为F，过点(0，－1)作直线L交抛物线A、B两点，再以AF、BF为邻边作平行四边形FARB，试求动点R的轨迹方程. 18．已知抛物线C：  ，过C上一点M，且与M处的切线垂直的直线称为C在点M的法线．（1）若C在点M的法线的斜率为  ，求点M的坐标（x0，y0）；（2）设P（－2，a）为C对称轴上的一点，在C上是否存在点，使得C在该点的法线通过点P？若有，求出这些点，以及C在这些点的法线方程；若没有，请说明理由. 参考答案： 经典例题：【解】(1) 解方程组  得  或  即A(－4,－2),B(8,4), 从而AB的中点为M(2,1).由kAB== ,直线AB的垂直平分线方程y－1= (x－2). 令y=－5, 得x=5, ∴Q(5,－5)．(2) 直线OQ的方程为x+y=0, 设P(x, x2－4).∵点P到直线OQ的距离d=  = , ,∴SΔOPQ=  = .∵P为抛物线上位于线段AB下方的点, 且P不在直线OQ上, ∴－4≤x<4  －4或4－4<x≤8.∵函数y=x2+8x－32在区间[－4,8] 上单调递增, ∴当x=8时, ΔOPQ的面积取到最大值30． 当堂练习： 1.C; 2.D; 3.A; 4.B; 5.B; 6.A; 7.C; 8.B; 9.C; 10.D; 11.  ; 12. 2; 13.  ;14. （2），（5）;15．[解析]：（1）由点A（2，8）在抛物线 上，有 ，解得p=16. 所以抛物线方程为  ，焦点F的坐标为（8，0）.（2）如图，由于F（8，0）是△ABC的重心，M是BC的中点，所以F是线段AM的 定比分点，且  ，设点M的坐标为 ，则 ，解得 ，所以点M的坐标为（11，－4）． （3）由于线段BC的中点M不在x轴上，所以BC所在 的直线不垂直于x轴.设BC所在直线的方程为：  由  消x得 ，所以  ，由（2）的结论得 ，解得 因此BC所在直线的方程为：  16．[解析]：设在抛物线y=ax2－1上关于直线x+y=0对称的相异两点为P(x,y),Q(－y,－x)，则   ，由①－②得x+y=a(x+y)(x－y),∵P、Q为相异两点，∴x+y≠0，又a≠0，∴  ，代入②得a2x2－ax－a+1=0，其判别式△=a2－4a2(1－a)＞0，解得 ．17．[解析]：设R(x,y),∵F(0,1), ∴平行四边形FARB的中心为  ，L:y=kx－1,代入抛物线方程得x2－4kx+4=0, 设A(x1,y1),B(x2,y2),则x1+x2=4k,x1x2=4，且△=16k2－16＞0，即|k|＞1 ①， ，∵C为AB的中点.∴    ，消去k得x2=4(y+3),由① 得， ，故动点R的轨迹方程为x2=4(y+3)( )．18． [解析]：（1）由题意设过点M的切线方程为：  ，代入C得 ，则  ， ，即M（－1，）．（2）当a＞0时，假设在C上存在点 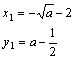 满足条件．设过Q的切线方程为： ，代入 ，则 ，且   ．若 时，由于 ，∴  或  ；若k=0时，显然 也满足要求．∴有三个点（－2＋  ， ），（－2－， ）及（－2，－ ），且过这三点的法线过点P（－2，a），其方程分别为： x＋2 y＋2－2a＝0，x－2y＋2＋2a＝0，x＝－2.当a≤0时，在C上有一个点（－2，－ ），在这点的法线过点P（－2，a），其方程为：x＝－2.(责任编辑：admin) |