|
谈椭圆扁平的判定 广东省中山一中高中部 许少华 我们知道,椭圆的离心率 探究一:能否借助 首先,我们来看能否用 再看能否用 显然,既可以用 探究二:为什么选用 第一,椭圆的“圆”的程度用 第二,对于椭圆, 探究三: 例1、设椭圆的两个焦点分别为 (A) 解析:设椭圆方程为 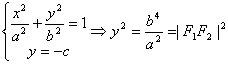 即 即评析:本题重在产生关于 例2、椭圆 (A) 解析:此题的本质是椭圆的两个顶点  评析:建立在条件的基础上,产生关于 例3、已知c是椭圆 (A)(1,+∞) (B)( 解析:由 于是得答案(D); 评析:如何求 例4、已知椭圆 解析一 设点 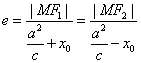 ,又由已知可得: ,又由已知可得: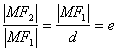 ,则有: ,则有:考虑椭圆离心率 解析二 由 评析:离心率的最值也是我们经常遇到的问题,在最值的求解过程中,抓问题的转折点很关键,解一中“ 好了,经过这一番的探究,你有收获吗? (责任编辑:admin) |
